题目内容
如图,在棱长为2的正方体ABCD—A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点.那么异面直线OE和FD1所成角的余弦值为( )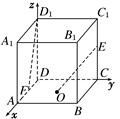
A.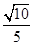 | B.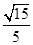 |
C.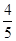 | D.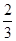 |
B
解析试题分析:建立如图所示空间直角坐标系,
则O(1,1,0),E(0,2,1),F(1,0,0), (0,0,2),
(0,0,2),
所以 =(-1,-0,2),
=(-1,-0,2), =(-1,-1,1),
=(-1,-1,1), =
=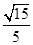 ,故选B。
,故选B。
考点:本题主要考查异面直线所成角的计算。
点评:基础题,求异面直线所成角应用“几何法”要遵循“一作、二证、三计算”。利用空间向量可转化成向量的计算问题。

练习册系列答案
相关题目
已知两个不同的平面α, 和两条不重合的直线m,n,则下列四种说法正确的为( )
和两条不重合的直线m,n,则下列四种说法正确的为( )
A.若m∥n,n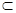 α,则m∥α α,则m∥α |
| B.若m⊥n,m⊥α,则n∥α |
C.若m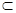 α,n α,n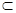  ,α∥ ,α∥ ,则m,n为异面直线 ,则m,n为异面直线 |
D.若α⊥ ,m⊥α,n⊥ ,m⊥α,n⊥ ,则m⊥n ,则m⊥n |
若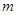 、
、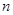 是两条不同的直线,
是两条不同的直线,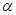 、
、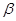 是两个不同的平面,则下列命题中不正确的是( )
是两个不同的平面,则下列命题中不正确的是( )
A.若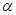 ∥ ∥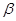 , ,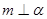 ,则 ,则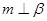 |
B.若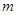 ∥ ∥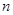 , ,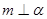 ,则 ,则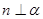 |
C.若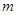 ∥ ∥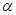 , ,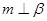 ,则 ,则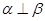 |
D.若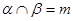 , ,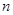 与 与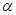 、 、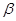 所成的角相等,则 所成的角相等,则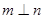 |
已知正四棱柱 中,
中, ,E为
,E为 中点,则异面直线BE与
中点,则异面直线BE与 所成角的余弦值为( )
所成角的余弦值为( )
A. | B. | C. | D. |
已知两条不同的直线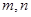 ,两个不同的平面
,两个不同的平面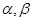 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.若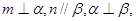 则 则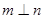 |
B.若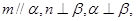 则 则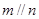 |
C.若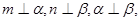 则 则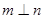 |
D.若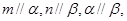 则 则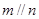 |
正方体的一条对角线与正方体的棱可组成n对异面直线,则n等于 ( )
| A.2 | B.3 | C.6 | D.12 |
设m、n是两条不同的直线, 、β是两个不同的平面,则下列命题中正确的是
、β是两个不同的平面,则下列命题中正确的是
A.若m∥n,m∥ ,则n∥ ,则n∥ |
B.若 ⊥β,m∥ ⊥β,m∥ ,则m⊥β ,则m⊥β |
C.若 ⊥β,m⊥β,则m∥ ⊥β,m⊥β,则m∥ |
D.若m⊥n,m⊥ ,n⊥β,则 ,n⊥β,则 ⊥β ⊥β |
已知直线 、
、 、
、 不重合,平面
不重合,平面 、
、 不重合,下列命题正确的是( )
不重合,下列命题正确的是( )
A.若 , , , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若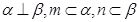 ,则 ,则 |
D.若 ,则 ,则 |
( )已知两个不同的平面 、
、 ,能判定
,能判定 //
// 的条件是
的条件是
A. 、 、 分别平行于直线 分别平行于直线 | B. 、 、 分别垂直于直线 分别垂直于直线 |
C. 、 、 分别垂直于平面 分别垂直于平面 | D. 内有两条直线分别平行于 内有两条直线分别平行于 |