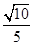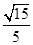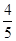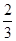题目内容
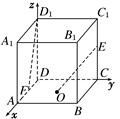
已知正四棱柱 中,
中, ,E为
,E为 中点,则异面直线BE与
中点,则异面直线BE与 所成角的余弦值为( )
所成角的余弦值为( )
A. | B. | C. | D. |
C
解析试题分析:连接A1B,则∠A1BE即为异面直线BE与 所成的角,设
所成的角,设 ,则BE=
,则BE=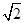 ,A1B=
,A1B= ,在三角形A1BE中,由余弦定理得:
,在三角形A1BE中,由余弦定理得: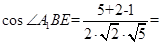
 。
。
考点:异面直线所成的角;余弦定理。
点评:我们可以通过直线平移找出异面直线所成的角,属于常见题型,也是基础题。

练习册系列答案
相关题目
如图,在正四棱柱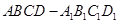 中,
中,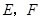 分别是
分别是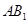 ,
,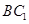 的中点,则以下结论中不成立的是( )
的中点,则以下结论中不成立的是( )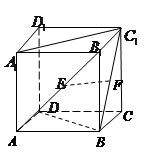
A.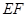 与 与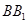 垂直 垂直 | B.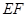 与 与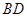 垂直 垂直 |
C.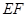 与 与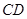 异面 异面 | D.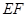 与 与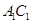 异面 异面 |
设 、b是两条不同的直线,
、b是两条不同的直线, 、
、 是两个不同的平面,则下列四个命题中正确的是( )
是两个不同的平面,则下列四个命题中正确的是( )
A.若 ⊥b, ⊥b, ⊥ ⊥ ,则b∥ ,则b∥ | B.若 ∥ ∥ , , ⊥ ⊥ ,则 ,则 ⊥ ⊥ |
C.若 ⊥ ⊥ , , ⊥ ⊥ ,则 ,则  ∥ ∥ | D.若 ⊥b, ⊥b, ⊥ ⊥ ,b⊥ ,b⊥ ,则 ,则 ⊥ ⊥ |
设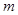 、
、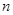 为两条不重合的直线,
为两条不重合的直线,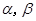 为两个不重合的平面,下列命题中正确命题的是
为两个不重合的平面,下列命题中正确命题的是
A.若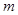 、 、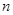 与 与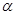 所成的角相等,则 所成的角相等,则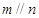 |
B.若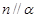 , ,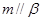 , ,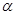 ∥ ∥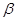 ,则 ,则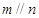 |
C.若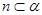 , ,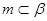 , ,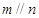 ,则 ,则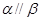 |
D.若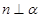 , ,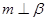 , ,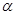 ⊥ ⊥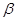 ,则 ,则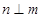 |
设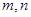 是两条不同的直线,
是两条不同的直线, 是三个不同的平面.给出下列四个命题:
是三个不同的平面.给出下列四个命题:
①若 ⊥
⊥ ,
,  ,则
,则 ;
;
②若 ,则
,则 ;
;
③若 ,则
,则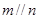 ;
;
④若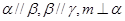 ,则
,则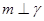 .
.
其中正确命题的序号是( )
| A.①和② | B.②和③ | C.③和④ | D.①和④ |
已知三条直线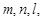 三个平面
三个平面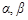 ,r,下列四个命题中正确的是( )
,r,下列四个命题中正确的是( )
A.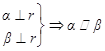 | B.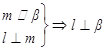 |
C. | D.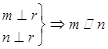 |
如图,已知正方体ABCD-A1B1C1D1,E、F分别是平面A1B1C1D1和ADD1A1的中心,则EF和CD所成的角是( ).
| A.60° | B.45° | C.30° | D.90° |
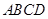 沿对角线
沿对角线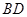 折成直二面角
折成直二面角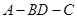 ,有如下四个结论:
,有如下四个结论: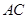 ⊥
⊥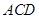 是等边三角形;
是等边三角形;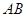 与平面
与平面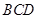 所成的角为60°; ④
所成的角为60°; ④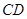 所成的角为60°.
所成的角为60°.