题目内容
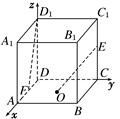
正方体的一条对角线与正方体的棱可组成n对异面直线,则n等于 ( )
| A.2 | B.3 | C.6 | D.12 |
C
解析试题分析:画出正方体,做出一条对角线,结合异面直线的定义,可以判断出有6对异面直线。
考点:异面直线
点评:画图较形象,有助解题。本题考查异面直线,属基础题。

练习册系列答案
相关题目
设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题中正确的是
| A.若m∥n,m∥α,则n∥α | B.若α⊥β,m∥α,则m⊥β |
| C.若α⊥β,m⊥β,则m∥α | D.若m⊥n,m⊥α, n⊥β,则α⊥β |
设 、b是两条不同的直线,
、b是两条不同的直线, 、
、 是两个不同的平面,则下列四个命题中正确的是( )
是两个不同的平面,则下列四个命题中正确的是( )
A.若 ⊥b, ⊥b, ⊥ ⊥ ,则b∥ ,则b∥ | B.若 ∥ ∥ , , ⊥ ⊥ ,则 ,则 ⊥ ⊥ |
C.若 ⊥ ⊥ , , ⊥ ⊥ ,则 ,则  ∥ ∥ | D.若 ⊥b, ⊥b, ⊥ ⊥ ,b⊥ ,b⊥ ,则 ,则 ⊥ ⊥ |
设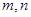 是两条不同的直线,
是两条不同的直线, 是三个不同的平面.给出下列四个命题:
是三个不同的平面.给出下列四个命题:
①若 ⊥
⊥ ,
,  ,则
,则 ;
;
②若 ,则
,则 ;
;
③若 ,则
,则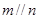 ;
;
④若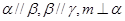 ,则
,则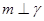 .
.
其中正确命题的序号是( )
| A.①和② | B.②和③ | C.③和④ | D.①和④ |
如图在长方体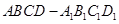 中,其中
中,其中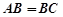 ,
,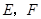 分别是
分别是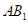 ,
, 的中点,则以下结论中
的中点,则以下结论中
① 与
与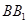 垂直; ②
垂直; ② ⊥平面
⊥平面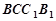 ;
;
③ 与
与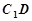 所成角为
所成角为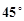 ; ④
; ④ ∥平面
∥平面
不成立的是( )
| A.②③ | B.①④ | C.③ | D.①②④ |
已知三条直线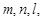 三个平面
三个平面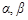 ,r,下列四个命题中正确的是( )
,r,下列四个命题中正确的是( )
A.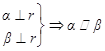 | B.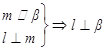 |
C. | D.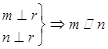 |
设l,m,n为三条不同的直线,α、β为两个不同的平面,下列命题中正确的个数是( )
① 若l⊥α,m∥β,α⊥β则l⊥m ② 若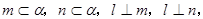 则l⊥α
则l⊥α
③ 若l∥m,m∥n,l⊥α,则n⊥α ④ 若l∥m,m⊥α,n⊥β,α∥β,则l∥n
| A.1 | B.2 | C.3 | D.4 |
直线a、b、c及平面α、β,下列命题正确的是( )
A.若a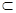 α,b α,b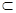 α,c⊥a, c⊥b 则c⊥α α,c⊥a, c⊥b 则c⊥α | B.若b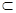 α, a//b则 a//α α, a//b则 a//α |
| C.若a//α,α∩β=b则a//b | D.若a⊥α, b⊥α 则a//b |