题目内容
设m、n是两条不同的直线, 、β是两个不同的平面,则下列命题中正确的是
、β是两个不同的平面,则下列命题中正确的是
A.若m∥n,m∥ ,则n∥ ,则n∥ |
B.若 ⊥β,m∥ ⊥β,m∥ ,则m⊥β ,则m⊥β |
C.若 ⊥β,m⊥β,则m∥ ⊥β,m⊥β,则m∥ |
D.若m⊥n,m⊥ ,n⊥β,则 ,n⊥β,则 ⊥β ⊥β |
D
解析试题分析:A.若m∥n,m∥ ,则n∥
,则n∥ 或者 n
或者 n 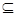
 ;
;
B.若 ⊥β,m∥
⊥β,m∥ ,则m与β可能平行,可能相交,也可能在平面内。
,则m与β可能平行,可能相交,也可能在平面内。
C.若 ⊥β,m⊥β,则m∥
⊥β,m⊥β,则m∥ 或者 m
或者 m 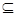
 ;
;
D.若m⊥n,m⊥ ,n⊥β,则
,n⊥β,则 ⊥β,此命题正确。
⊥β,此命题正确。
考点:线面平行的判定定理;空间中线、面的位置关系。
点评:本小题主要考查空间中线、面的各种位置关系,解题时要灵活运用立体几何中各位置关系的判定定理和性质定理,并借助空间想象寻找反例,判断命题的真假,这种类型的问题在高考选择题中非常普遍.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设直线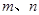 和平面
和平面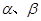 ,下列四个命题中,正确的是( )
,下列四个命题中,正确的是( )
A.若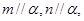 则 则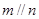 | B.若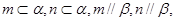 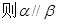 |
C.若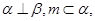 则 则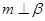 | D.若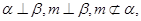 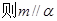 |
设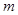 、
、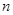 为两条不重合的直线,
为两条不重合的直线,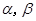 为两个不重合的平面,下列命题中正确命题的是
为两个不重合的平面,下列命题中正确命题的是
A.若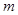 、 、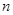 与 与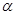 所成的角相等,则 所成的角相等,则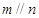 |
B.若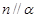 , ,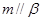 , ,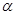 ∥ ∥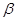 ,则 ,则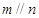 |
C.若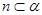 , ,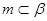 , ,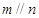 ,则 ,则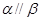 |
D.若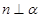 , ,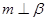 , ,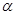 ⊥ ⊥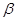 ,则 ,则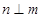 |
设m、n表示不同直线, 、
、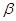 表示不同平面,下列命题正确的是 ( )
表示不同平面,下列命题正确的是 ( )
A.若m‖ ,m‖ n,则n‖ ,m‖ n,则n‖ |
B.若m  ,n ,n  ,m‖ ,m‖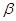 ,n‖ ,n‖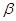 ,则 ,则 ‖ ‖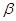 |
C.若  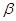 , m , m  ,m ,m n,则n‖ n,则n‖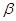 |
D.若  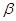 , m , m  ,n‖m,n ,n‖m,n 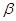 ,则n‖ ,则n‖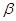 |
已知三条直线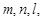 三个平面
三个平面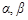 ,r,下列四个命题中正确的是( )
,r,下列四个命题中正确的是( )
A.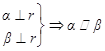 | B.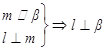 |
C. | D.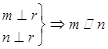 |
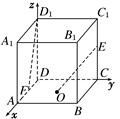
如图,长方体ABCD-A1B1C1D1中,AB=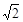 ,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )
,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )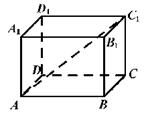
| A.30° | B.45° | C.60° | D.90° |
设 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
已知二面角 是直二面角,P为棱AB上一点,PQ、PR分别在平面
是直二面角,P为棱AB上一点,PQ、PR分别在平面 、
、 内,且
内,且 ,则
,则 为( )
为( )
| A.45° | B.60° | C.120° | D.150° |