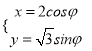Question

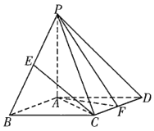
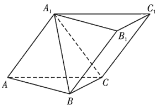
【题目】为了提升学生“数学建模”的核心素养，某校数学兴趣活动小组指导老师给学生布置了一项探究任务：如图，有一张边长为27cm的等边三角形纸片ABC，从中裁出等边三角形纸片作为底面，从剩余梯形中裁出三个全等的矩形作为侧面，围成一个无盖的三棱柱（不计损耗）．

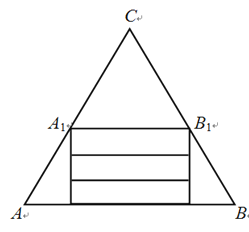
（1）若三棱柱的侧面积等于底面积，求此三棱柱的底面边长；

（2）当三棱柱的底面边长为何值时，三棱柱的体积最大？

Answer 1

【答案】（1）18cm（2）18cm

【解析】

(1) 设三棱柱的底面边长为,再根据三角形中的关系表达出底面积和与侧面积的关系式再解方程即可.

(2)同(1)可知,再求导分析函数的单调性求最大值即可.

设三棱柱的底面边长为,即,

则.

因为为等边三角形,

所以三棱柱的高为.

（1）因为三棱柱的底面积为,

侧面积为,

所以,

解得或（舍去）.

即三棱柱的底面边长为18cm.

（2）三棱柱的体积.

因为,,

所以.

因为,

所以当时,,故单调递增;

当时,,故单调递减.

所以当时,取到极大值,也是最大值,

.

即当底面边长为18cm时,三棱柱的体积最大,为.