题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以原点
).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)若直线![]() 与圆
与圆![]() 有公共点,试求实数
有公共点,试求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,过点
时,过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交圆
交圆![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)根据极坐标与普通方程的互化公式求出直线的直角坐标方程,消参得出圆的普通方程, 直线![]() 与圆
与圆![]() 有公共点,则圆心到直线的距离
有公共点,则圆心到直线的距离![]() ,即可求出范围;(2)将直线的参数方程代入曲线方程,根据t的几何意义求值即可.
,即可求出范围;(2)将直线的参数方程代入曲线方程,根据t的几何意义求值即可.
试题解析:
(1)由![]() ,
,
得![]() ,
,
即![]() ,
,
故直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
由![]()
得![]()
所以圆![]() 的普通方程为
的普通方程为![]() .
.
若直线![]() 与圆
与圆![]() 有公共点,则圆心
有公共点,则圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,即
,即![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .
.
(2)因为直线![]() 的倾斜角为
的倾斜角为![]() ,且过点
,且过点![]() ,
,
所以直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),①
为参数),①
圆![]() 的方程为
的方程为![]() ,②
,②
联立①②,得![]() ,
,
设![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,
,
则![]() ,
,![]() ,
,
故![]() .
.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 为菱形,
为菱形,![]() 在侧面
在侧面![]() 上的投影恰为
上的投影恰为![]() 的中点
的中点![]() ,
,![]() 为
为![]() 的中点.
的中点.
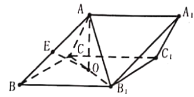
(Ⅰ)证明:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若![]() ,
,![]() 在线段
在线段![]() 上是否存在点
上是否存在点![]() (
(![]() 不与
不与![]() ,
,![]() 重合)使得直线
重合)使得直线![]() 与平面
与平面![]() 成角的正弦值为
成角的正弦值为![]() 若存在,求出
若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费对年销售量(单位:![]() )的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费
)的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费![]() (万元)和年销售量
(万元)和年销售量![]() (单位:
(单位:![]() )具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.
)具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.
| 2 | 4 | 5 | 3 | 6 |
| 2.5 | 4 | 4.5 | 3 | 6 |
(1)根据表中数据建立年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() ,根据(1)中的结果回答下列问题:
,根据(1)中的结果回答下列问题:
①当年宣传费为10万元时,年销售量及年利润的预报值是多少?
②估算该公司应该投入多少宣传费,才能使得年利润与年宣传费的比值最大.
附:问归方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为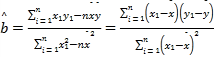 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.