题目内容
【题目】已知函数![]() 的部分图象如图所示,其中点
的部分图象如图所示,其中点![]() 的坐标为
的坐标为![]() .
.
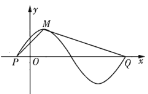
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)8(2)![]()
【解析】
(1)先根据点![]() 在函数
在函数![]() 的图象上及
的图象上及![]() 的图象特征得到
的图象特征得到![]() 的值,即可求得函数
的值,即可求得函数![]() 的最小正周期;
的最小正周期;
(2)可以根据![]() ,利用两角和的余弦公式进行求解,也可以在三角形中利用余弦定理进行求解,还可以借助向量进行求解.
,利用两角和的余弦公式进行求解,也可以在三角形中利用余弦定理进行求解,还可以借助向量进行求解.
(1)因为点![]() 在函数
在函数![]() 的图象上,即
的图象上,即![]() ,
,
所以![]() ,即
,即![]() .
.
由题意可知函数![]() 的最小正周期
的最小正周期![]() ,
,
所以![]() ,解得
,解得![]() .
.
又![]() ,所以
,所以![]() ,
,
所以函数![]() 的最小正周期
的最小正周期![]() .
.
(2)解法一:如图,

过点![]() 作
作![]() 轴于点
轴于点![]() ,由(1)知
,由(1)知![]() .
.
令![]() ,得
,得![]() ,得
,得![]() ,
,
所以![]() ,
,
所以![]() ,
,
![]() ,
,
所以![]()
![]() ,
,
所以![]() ,即
,即![]() ,
,
又![]() ,
,
所以![]() 或
或![]() (舍去).
(舍去).
所以![]() ,
,
所以![]() .
.
解法二:过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
由(1)知,函数![]() 的最小正周期
的最小正周期![]() ,又
,又![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以在![]() 中,
中,![]() ,
,
即 ,
,
化简得![]() ,即
,即![]() ,
,
所以![]() 或
或![]() (舍去).
(舍去).
所以![]() ,
,
所以![]() .
.
解法三:过点![]() 作
作![]() 轴于
轴于![]() ,
,
由(1)知![]() ,
,
令![]() ,得
,得![]() ,得
,得![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
所以![]() ,
,
故![]() .
.

【题目】现在进入“互联网+”时代,大学生小张自己开了一家玩具店,他通过“互联网+”销售某种玩具,经过一段时间对一种玩具的销售情况进行统计,得5数据如下:
假定玩具的销售量![]() (百个)与玩具的销售价价格
(百个)与玩具的销售价价格![]() (元)之间存在相关关系:
(元)之间存在相关关系:
销售量 | 2 | 3 | 4 | 5 | 6 | 8 |
单个玩具的销售价 | 5.5 | 4.3 | 3.9 | 3.8 | 3.7 | 3.6 |
根据以上数据,小张分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)以![]() 为解释变量,
为解释变量,![]() 为预报变量,作出散点图;
为预报变量,作出散点图;
(2)分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
,![]() 大小,判断哪个模型拟后效果更好.
大小,判断哪个模型拟后效果更好.
(3)若—个玩具进价0.5元,依据(2)中拟合效果好的模型判断该玩具店有无亏损的可能?
【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每个人每日健步的步数,从而为科学健身提供一定的帮助.某市工会为了解该市市民每日健步走的情况,从本市市民中随机抽取了2000名市民(其中不超过40岁的市民恰好有1000名),利用手机计步软件统计了他们某天健步的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九组(单位:千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如右,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
九组(单位:千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如右,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
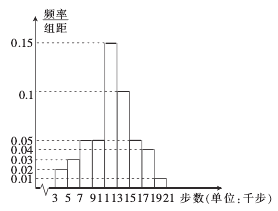
分组 (单位:千步) |
|
|
|
|
|
|
|
|
|
频数 | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
(1)现规定,日健步步数不低于13000步的为“健步达人”,填写下面列联表,并根据列联表判断能否有![]() %的把握认为是否为“健步达人”与年龄有关;
%的把握认为是否为“健步达人”与年龄有关;
健步达人 | 非健步达人 | 总计 | |
40岁以上的市民 | |||
不超过40岁的市民 | |||
总计 |
(2)(ⅰ)利用样本平均数和中位数估计该市不超过40岁的市民日健步步数(单位:千步)的平均数和中位数;
(ⅱ)由频率分布直方图可以认为,不超过40岁的市民日健步步数![]() (单位:千步)近似地服从正态分布
(单位:千步)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值),
(每组数据取区间的中点值),![]() 的值已求出约为
的值已求出约为![]() .现从该市不超过40岁的市民中随机抽取5人,记其中日健步步数
.现从该市不超过40岁的市民中随机抽取5人,记其中日健步步数![]() 位于
位于![]() 的人数为
的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
参考公式: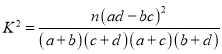 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
若![]() ,则
,则![]() ,
,![]() .
.