题目内容
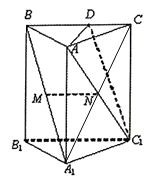
【题目】如图，在直三棱柱ABC﹣A1B1C1中，点M、N分别为线段A1B、AC1的中点． 
（1）求证：MN∥平面BB1C1C；
（2）若D在边BC上，AD⊥DC1 ， 求证：MN⊥AD．
【答案】
（1）证明：如图，连接A1C，在直三棱柱ABC﹣A1B1C1中，侧面AA1C1C为平行四边形，
又∵N分别为线段AC1的中点．
∴AC1与A1C相交于点N，即A1C经过点N，且N为线段A1C的中点，
∵M为线段A1B的中点，
∴MN∥BC，
又∵NN平面BB1C1C，BC平面BB1C1C，
∴MN∥平面BB1C1C
（2）证明：在直三棱柱ABC﹣A1B1C1中，CC1⊥平面ABC，
又AD平面ABC1，所以CC1⊥AD，
∵AD⊥DC1，DC1平面BB1C1C，CC1平面BB1C1C，CC1∩DC1=C1，
∴AD⊥平面BB1C1C，
又∵BC平面BB1C1C，
∴AD⊥BC，
又由（1）知，MN∥BC，
∴MN⊥AD
【解析】（1）由题意，利用三角形中位线定理可证MN∥BC，即可判定MN∥平面BB1C1C．（2）利用线面垂直的性质可证CC1⊥AD，结合已知可证AD⊥平面BB1C1C，从而证明AD⊥BC，结合（1）知，MN∥BC，即可证明MN⊥AD．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对直线与平面垂直的性质的理解，了解垂直于同一个平面的两条直线平行．
练习册系列答案
相关题目
