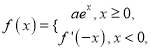题目内容
【题目】已知函数f(x)=|x﹣a|,g(x)=x2+2ax+1(a为正常数),且函数f(x)和g(x)的图象与y轴的交点重合.
(1)求a实数的值
(2)若h(x)=f(x)+b ![]() (b为常数)试讨论函数h(x)的奇偶性;
(b为常数)试讨论函数h(x)的奇偶性;
(3)若关于x的不等式f(x)﹣2 ![]() >a有解,求实数a的取值范围.
>a有解,求实数a的取值范围.
【答案】
(1)解:由题意得:
f(0)=g(0),
即|a|=1,
又∵a>0,
∴a=1
(2)解:由(1)可知,f(x)=|x﹣1|,
g(x)=x2+2x+1=(x+1)2,
∴h(x)=f(x)+b ![]()
=|x﹣1|+b|x+1|,
若h(x)为偶函数,即h(x)=h(﹣x),则有b=1,此时h(2)=4,h(﹣2)=4,
故h(2)≠﹣h(﹣2),即h(x)不为奇函数;
若h(x)为奇函数,即h(x)=﹣h(﹣x),则b=﹣1,此时h(2)=2,h(﹣2)=﹣2,
故h(2)≠h(﹣2),即h(x)不为偶函数;
综上,当且仅当b=1时,函数h(x)为偶函数,且不为奇函数,
当且仅当b=﹣1时,函数h(x)为奇函数,且不为偶函数,
当b≠±1时,函数h(x)既非奇函数又非偶函数
(3)解:关于x的不等式f(x)﹣2 ![]() >a有解,
>a有解,
即x的不等式|x﹣1|﹣2|x+1|>a有解
故|x﹣1|﹣2|x+1|的最大值大于或等于a,
画出函数y=|x﹣1|﹣2|x+1|的图象,如图所示:
由图象可知,|x﹣1|﹣2|x+1|的最大值为2,
∴a<2
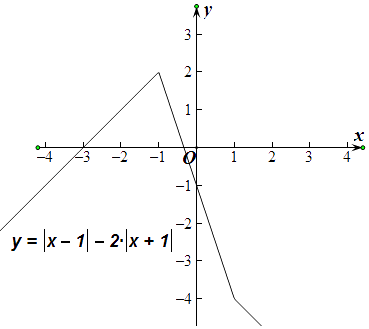
【解析】(1)由题意得:f(0)=g(0),即|a|=1,可得a=1.(2)利用奇偶函数的定义,确定b的值,进而可得函数的奇偶性.(3)关于x的不等式f(x)﹣2 ![]() >a有解转化为|x﹣1|﹣2|x+1|的最大值大于或等于a,画出函数画出函数y=|x﹣1|﹣2|x+1|的图象,由图象可得答案.
>a有解转化为|x﹣1|﹣2|x+1|的最大值大于或等于a,画出函数画出函数y=|x﹣1|﹣2|x+1|的图象,由图象可得答案.
【考点精析】解答此题的关键在于理解函数的奇偶性的相关知识,掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称.

【题目】某种多面体玩具共有12个面,在其十二个面上分别标有数字1,2,3,…,12.若该玩具质地均匀,则抛掷该玩具后,任何一个数字所在的面朝上的概率均相等.
为检验某批玩具是否合格,制定检验标准为:多次抛掷该玩具,并记录朝上的面上标记的数字,若各数字出现的频率的极差不超过0.05.则认为该玩具合格.

(1)对某批玩具中随机抽取20件进行检验,将每个玩具各面数字出现频率的极差绘制成茎叶图(如图所示),试估计这批玩具的合格率;
(2)现有该种类玩具一个,将其抛掷100次,并记录朝上的一面标记的数字,得到如下数据:
朝上面的数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
次数 | 9 | 7 | 8 | 6 | 10 | 9 | 9 | 8 | 10 | 9 | 7 | 8 |
1)试判定该玩具是否合格;
2)将该玩具抛掷一次,记事件![]() :向上的面标记数字是完全平方数(能写成整数的平方形式的数,如
:向上的面标记数字是完全平方数(能写成整数的平方形式的数,如![]() ,9为完全平方数);事件
,9为完全平方数);事件![]() :向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中
:向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中![]() 表示
表示![]() 的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件
的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件![]() 与事件
与事件![]() 有关.
有关.
|
| 合计 | |
| |||
| |||
合计 | 100 |
(参考公式及数据: 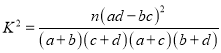 ,
, ![]() )
)