题目内容
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域上的任意实数
对其公共定义域上的任意实数![]() 都满足:
都满足: ![]() 和
和![]() 恒成立,则称此直线
恒成立,则称此直线![]() 为
为![]() 和
和![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() ,
, ![]() ,有下列命题:
,有下列命题:
①![]() 在
在![]() 内单调递增;
内单调递增;
②![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的最小值为-4;
的最小值为-4;
③![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的取值范围是
的取值范围是![]() ;
;
④![]() 和
和![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]() .
.
其中真命题的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】①![]() ,
, ![]() ,在
,在![]() 内单调递增,故①正确;②,③设
内单调递增,故①正确;②,③设![]() 的隔离直线为
的隔离直线为![]() ,则
,则![]() 对一切实数
对一切实数![]() 成立,即有
成立,即有![]() ,又
,又![]() 对一切
对一切![]() 成立,则
成立,则![]() ,即
,即![]() ,即有
,即有![]() 且
且![]() ,同理
,同理![]() 可得
可得![]() ,故②正确,③错误,④函数
,故②正确,③错误,④函数![]() 和
和![]() 的图象在
的图象在![]() 处有公共点,因此存在
处有公共点,因此存在![]() 和
和![]() 的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为
的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为![]() ,则隔离直线方程为
,则隔离直线方程为![]() ,即
,即![]() ,由
,由![]() ,可得
,可得![]() ,当
,当![]() 恒成立,则
恒成立,则![]() ,只有
,只有![]() ,此时直线方程为
,此时直线方程为![]() ,下面证明
,下面证明![]() ,令
,令![]()
![]() ,
, 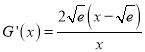 ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() 取到极小值,极小值是
取到极小值,极小值是![]() ,也是最小值,
,也是最小值, ![]() ,则
,则![]() ,
, ![]() 函数
函数![]() 和
和![]() 存在唯一的隔离直线
存在唯一的隔离直线![]() ,故④正确,真命题的个数有三个,故选C.
,故④正确,真命题的个数有三个,故选C.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
【题目】为缓减人口老年化带来的问题,中国政府在2016年1月1日作出全国统一实施全面的“二孩”政策,生“二孩”是目前中国比较流行的元素![]() 某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”
某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”![]() 现已得知100人中同意父母生“二孩”占
现已得知100人中同意父母生“二孩”占![]() ,统计情况如表:
,统计情况如表:
性别属性 | 同意父母生“二孩” | 反对父母生“二孩” | 合计 |
男生 | 10 | ||
女生 | 30 | ||
合计 | 100 |
![]() 请补充完整上述列联表;
请补充完整上述列联表;
![]() 根据以上资料你是否有
根据以上资料你是否有![]() 把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
参考公式与数据:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|