Question

【题目】已知正方体，在空间中到三条棱所在直线距离相等的点的个数（ ）

A. 0B. 2C. 3D. 无数个

Answer 1

【答案】D

【解析】

由于点D、B1显然满足要求，猜想B1D上任一点都满足要求，然后证明结论．

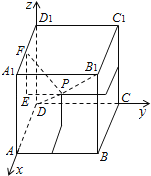
在正方体ABCD﹣A1B1C1D1上建立如图所示空间直角坐标系，

并设该正方体的棱长为1，连接B1D，并在B1D上任取一点P，

因为（1，1，1），

所以设P（a，a，a），其中0≤a≤1．

作PE⊥平面A1D，垂足为E，再作EF⊥A1D1，垂足为F，

则PF是点P到直线A1D1的距离．

所以PF；

同理点P到直线AB、CC1的距离也是．

所以B1D上任一点与正方体ABCD﹣A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离都相等，

所以与正方体ABCD﹣A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点有无数个．

故选：D．