Question

【题目】设是首项为a，公差为d的等差数列(d≠0)， 是其前n项的和.记，n∈N*，其中c为实数.

(1)若c＝0，且b1，b2，b4成等比数列，证明：Snk＝n2Sk(k，n∈N*)；

(2)若{}是等差数列，证明：c＝0.

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】试题分析：（1）由c＝0，且b1，b2，b4成等比数列，可得d＝2a，对于所有的m∈N*，有Sm＝m2a，从而对于所有的k，n∈N*，有Snk＝(nk)2a＝n2k2a＝n2Sk；

（2）设数列{bn}的公差为d1，则bn＝b1＋(n－1)d1，即b1＋(n－1)d1，代入＝na＋d,得n3＋(b1－d1－a＋d)n2＋cd1n＝c(d1－b1)，则对于所有的n∈N*，有An3＋Bn2＋cd1n＝D.(*)，在(*)式中分别取n＝1，2，3，4，列方程组求解即可.

试题解析：

由题设，Sn＝na＋d.

(1)由c＝0，得bn＝＝a＋d.

又b1，b2，b4成等比数列，所以b＝b1b4，

即＝a，化简得d2－2ad＝0.

因为d≠0，所以d＝2a.

因此，对于所有的m∈N*，有Sm＝m2a.

从而对于所有的k，n∈N*，有Snk＝(nk)2a＝n2k2a＝n2Sk.

(2)设数列{bn}的公差为d1，则bn＝b1＋(n－1)d1，

即＝b1＋(n－1)d1，n∈N*，代入Sn的表达式，

整理得，对于所有的n∈N*，有

n3＋(b1－d1－a＋d)n2＋cd1n＝c(d1－b1).

令A＝d1－d，B＝b1－d1－a＋d，D＝c(d1－b1)，则对于所有的n∈N*，有An3＋Bn2＋cd1n＝D.(*)

在(*)式中分别取n＝1，2，3，4，得

A＋B＋cd1＝8A＋4B＋2cd1＝27A＋9B＋3cd1＝64A＋16B＋4cd1，

从而有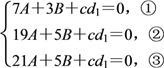

由②，③得A＝0，cd1＝－5B，代入方程①，得B＝0，从而cd1＝0.即d1－d＝0，b1－d1－a＋d＝0，cd1＝0.

若d1＝0，则由d1－d＝0，得d＝0，与题设矛盾，

所以d1≠0.又cd1＝0，所以c＝0.