题目内容
已知函数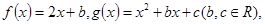 对任意的
对任意的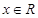 恒有
恒有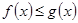 成立.
成立.
(1)记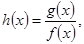 如果
如果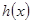 为奇函数,求b,c满足的条件;
为奇函数,求b,c满足的条件;
(2)当b=0时,记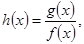 若
若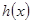 在
在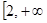 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围;
(3)证明:当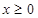 时,
时,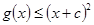 成立;
成立;
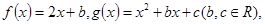 对任意的
对任意的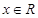 恒有
恒有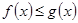 成立.
成立.(1)记
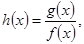 如果
如果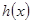 为奇函数,求b,c满足的条件;
为奇函数,求b,c满足的条件;(2)当b=0时,记
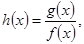 若
若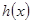 在
在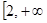 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围;(3)证明:当
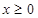 时,
时,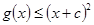 成立;
成立;(1) ;(2)
;(2) ;(3)证明见解析.
;(3)证明见解析.
 ;(2)
;(2) ;(3)证明见解析.
;(3)证明见解析.试题分析:(1)首先要讨论题设的先决条件
 对
对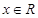 恒成立,
恒成立,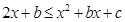 ,即
,即 恒成立,这是二次不等式,由二次函数知识,有
恒成立,这是二次不等式,由二次函数知识,有 ,化简之后有
,化简之后有 ,从而
,从而 .
.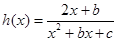 为
为 上的奇函数,可根据奇函数的必要条件有
上的奇函数,可根据奇函数的必要条件有 ,得
,得 ,则
,则 ,显然满足
,显然满足 ,
, 为奇函数,也可由
为奇函数,也可由 恒成立,也可求得
恒成立,也可求得 ;(2)
;(2) 时,
时, 在
在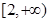 上是增函数,我们用增函数的定义,即设
上是增函数,我们用增函数的定义,即设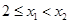 ,
, 恒成立,分析后得出
恒成立,分析后得出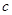 的范围;(3)
的范围;(3)
 ,问题变成证明
,问题变成证明 在
在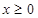 时恒成立,在
时恒成立,在 的情况下,
的情况下,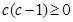 ,而
,而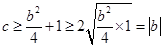 ,可见
,可见 ,那当
,那当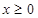 时,一定恒有
时,一定恒有 ,问题证毕.
,问题证毕.试题解析::(1)因为任意的
 恒有
恒有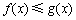 成立,
成立, 所以对任意的
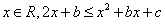 ,即
,即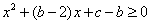 恒成立.
恒成立. 所以
 ,从而
,从而 .,即:
.,即: .
. 设
 的定义域为
的定义域为 ,因为
,因为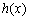 为奇函数,
为奇函数, 所以对于任意
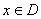 ,
, 成立.解得
成立.解得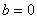 .
. 所以
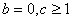 .
. (2)当
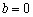 时,记
时,记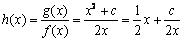 (
( )
) 因为
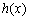 在
在 上为增函数,所以任取
上为增函数,所以任取 ,
,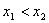 时,
时,  恒成立.
恒成立. 即任取
 ,
,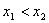 ,
, 成立,也就是
成立,也就是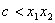 成立.
成立. 所以
 ,即
,即 的取值范围是
的取值范围是 .
. (3)由(1)得,
 且
且 ,
, 所以
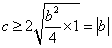 ,因此
,因此 .
.故当
 时,有
时,有 .
.即当
 时,
时,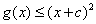 .
.
练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
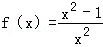 的定义域为E,值域为F.
的定义域为E,值域为F. 与集合F的关系;
与集合F的关系; },求实数a的值.
},求实数a的值.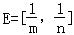 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.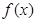 对任意实数
对任意实数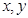 恒有
恒有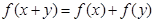 且当
且当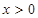 时,有
时,有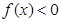 且
且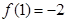 .
. 上的最大值;
上的最大值;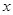 的不等式
的不等式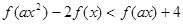 .
. ”,对任意
”,对任意 ,
,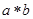 为唯一确定的实数,且具有性质:
为唯一确定的实数,且具有性质: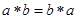 (2)对任意的
(2)对任意的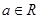 ,
,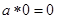 ;
;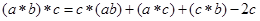
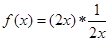 的性质,有如下说法:
的性质,有如下说法: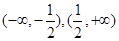 ,其中所有正确说法的个数( )
,其中所有正确说法的个数( )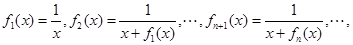 则函数
则函数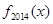 是( )
是( )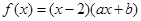 为偶函数,且在
为偶函数,且在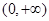 单调递增,则
单调递增,则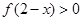 的解集为( )
的解集为( )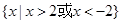
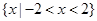
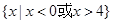
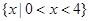
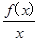 ,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.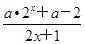 (x∈R),试确定a的值,使f(x)为奇函数;
(x∈R),试确定a的值,使f(x)为奇函数;