题目内容
9.曲线C1:$\frac{|x|}{4}$-$\frac{|y|}{2}$=1与曲线C2:$\frac{|x|}{8}$+$\frac{|y|}{2}$=1所围成图形的面积为$\frac{16}{3}$.分析 根据题意,在同一坐标系中画出C1、C2所围成的图形,根据图形的对称性求出它的面积即可.
解答 解:对于曲线C1:$\frac{|x|}{4}$-$\frac{|y|}{2}$=1,
当x>0,y>0时,$\frac{x}{4}$-$\frac{y}{2}$=1,
当x>0,y<0时,$\frac{x}{4}$+$\frac{y}{2}$=1,
当x<0,y<0时,$\frac{x}{4}$-$\frac{y}{2}$=-1,
当x<0,y>0时,$\frac{x}{4}$+$\frac{y}{2}$=-1;
对于曲线C2:$\frac{|x|}{8}$+$\frac{|y|}{2}$=1,
当x>0,y>0时,$\frac{x}{8}$+$\frac{y}{2}$=1,
当x>0,y<0时,$\frac{x}{8}$-$\frac{y}{2}$=1,
当x<0,y<0时,$\frac{x}{8}$+$\frac{y}{2}$=-1,
当x<0,y>0时,$\frac{x}{8}$-$\frac{y}{2}$=-1;
在同一坐标系中画出这8条线段,它们所围成的图形是四边形ABCD和四边形EFGH,
如图所示;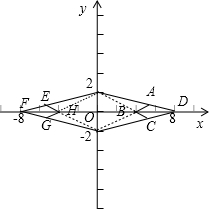
由$\left\{\begin{array}{l}{\frac{x}{4}-\frac{y}{2}=1}\\{\frac{x}{8}+\frac{y}{2}=1}\end{array}\right.$,得点A($\frac{16}{3}$,$\frac{2}{3}$);
∴△ABC的面积为:S△ABD=$\frac{1}{2}$BD•yA=$\frac{1}{2}$×4×$\frac{2}{3}$=$\frac{4}{3}$;
∴四边形ABCD的面积为:S四边形ABCD=2S△ABD=2S△ABD=2×$\frac{4}{3}$=$\frac{8}{3}$;
由C1、C2所围成的图形的面积为:
S=S四边形ABCD+S四边形EFGH=2×$\frac{8}{3}$=$\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 本题考查了直线方程的应用问题,也考查了分类讨论的应用问题,考查了数形结合的应用问题,是综合性题目.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案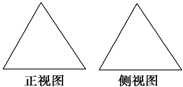 如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )
如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
| A. | 若α⊥β,m∥α,则m⊥β | B. | 若m∥α,n∥m,则n∥α | ||
| C. | 若m∥α,n∥β,且m∥n,则α∥β | D. | 若m⊥β,m∥α,则α⊥β |
| A. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{3}$] | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{2}}{3}$,$\frac{\sqrt{3}}{3}$] |
 设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )
设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )| A. | f(-1) | B. | f(-2) | C. | f(1) | D. | f(2) |