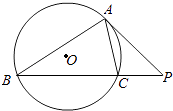[题目]如图.梯形中. .矩形所在的平面与平面垂直.且．(Ⅰ)求证:平面平面,(Ⅱ)若为线段上一点.平面与平面所成的锐二面角为.求的最小值．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，梯形中，，矩形所在的平面与平面垂直，且．

（Ⅰ）求证：平面平面；

（Ⅱ）若为线段上一点，平面与平面所成的锐二面角为，求的最小值．

【答案】（1）见解析（2）

【解析】试题分析：(1) 取中点，由题意可知四边形BCDM,ADCM均菱形，所以，即AD垂直于再垂直平面的交线，所以平面BFED，可证平面平面。（2）以DA,DB，DE分别为x,y,z轴建立空间直角坐标系，，用夹量建立函数关系所以

试题解析：（Ⅰ）取中点,连接,因为AB//CD,

所以四边形为菱形, 所以,

因为平面BFED⊥平面ABCD, 平面BFED平面ABCD ,

平面,所以平面BFED.

又平面ADE, ∴平面平面;

（Ⅱ）因为四边形BFED为矩形,所以ED⊥DB,

如图建立空间直角坐标系D-xyz.

设AD=1,则

,设是平面PAB的

法向量,则

取

又平面的一个法向量为

练习册系列答案

	做不到“光盘”行动	做到“光盘”行动
男	45	10
女	30	15

P（K2≥k0）	0.10	0.05	0.025
k0	2.706	3.841	5.024

经计算：K2= ≈3.03，参考附表，得到的正确结论是（）
A.有95%的把握认为“该学生能否做到光盘行到与性别有关”
B.有95%的把握认为“该学生能否做到光盘行到与性别无关”
C.有90%的把握认为“该学生能否做到光盘行到与性别有关”
D.有90%的把握认为“该学生能否做到光盘行到与性别无关”

【题目】如图，△ABC的顶点都在圆O上，点P在BC的延长线上，且PA与圆O切于点A．

（1）若∠ACB=70°，求∠BAP的度数；
（2）若 = ，求的值．

【题目】已知数列{an}的前n项和为Sn ，且Sn= + ．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足bn=an+2﹣an+ ，且数列{bn}的前n项和为Tn ，求证：Tn＜2n+ ．

【题目】已知数列{an}，{bn}，Sn为数列{an}的前n项和，向量 =（1，bn）， =（an﹣1，Sn）， ∥ ．
（1）若bn=2，求数列{an}通项公式；
（2）若bn= ，a2=0．
①证明：数列{an}为等差数列；
②设数列{cn}满足cn= ，问是否存在正整数l，m（l＜m，且l≠2，m≠2），使得cl、c2、cm成等比数列，若存在，求出l、m的值；若不存在，请说明理由．

【题目】如图，已知直四棱柱ABCD﹣A1B1C1D1的底面ABCD为菱形，且∠BCD=60°，P为AD1的中点，Q为BC的中点

（1）求证：PQ∥平面D1DCC1；
（2）求证：DQ⊥平面B1BCC1 ．

【题目】某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，220），[220.240），[240，260），[260，280），[280，300）分组的频率分布直方图如图．

（1）求直方图中x的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，[220，240），[240，260），[260，280），[280，300）的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220，240）的用户中应抽取多少户？

【题目】某班同学准备参加学校在寒假里组织的“社区服务”、“进敬老院”、“参观工厂”、“民俗调查”、“环保宣传”五个项目的社会实践活动，每天只安排一项活动，并要求在周一至周五内完成.其中“参观工厂”与“环保宣讲”两项活动必须安排在相邻两天，“民俗调查”活动不能安排在周一.则不同安排方法的种数是（）

A.48 B.24 C.36 D.64

【题目】设双曲线 =1（a＞0，b＞0）的右焦点为F，右顶点为A，过F作AF的垂线与双曲线的两条渐近线交于B、C两点，过B、C分别作AC、AB的垂线，两垂线交于点D．若D到直线BC的距离小于2（a+ ），则该双曲线的离心率的取值范围是（）
A.（1，2）
B.（，2）
C.（1，）
D.（，）

试题分类