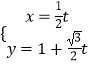题目内容
【题目】已知数列{an}的前n项和为Sn , 且Sn= ![]() +
+ ![]() .
.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an+2﹣an+ ![]() ,且数列{bn}的前n项和为Tn , 求证:Tn<2n+
,且数列{bn}的前n项和为Tn , 求证:Tn<2n+ ![]() .
.
【答案】
(1)解:当n≥2时,
an=Sn﹣Sn﹣1
= ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]()
=n+1,
又n=1时,
a1=S1=2适合an=n+1,
∴an=n+1
(2)证明:由(1)知:
bn=n+3﹣(n+1)+ ![]()
=2+ ![]() ×(
×( ![]() ﹣
﹣ ![]() ),
),
∴Tn=b1+b2+b3+…+bn
=2n+ ![]() ×(
×( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
=2n+ ![]() ×(
×( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )
)
<2n+ ![]() :
:
【解析】(1)根据数列的通项an和Sn的关系,即可求解数列{an}的通项公式;(2)由bn=2+ ![]() (
( ![]() ﹣
﹣ ![]() ),即可利用裂项相消求解数列的和,得以证明.
),即可利用裂项相消求解数列的和,得以证明.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系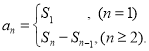 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】【2017重庆二诊】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
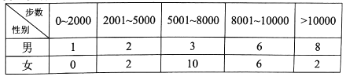
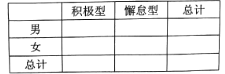
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 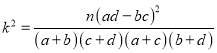 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.