题目内容
(本题满分13分)已知定义在正实数集上的函数 ,
, ,其中
,其中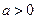 . 设两曲线
. 设两曲线 ,
, 有公共点,且在该点处的切线相同.(I)用
有公共点,且在该点处的切线相同.(I)用 表示
表示 ;(II)求证:
;(II)求证: (
( ).
).
 ,
, ,其中
,其中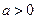 . 设两曲线
. 设两曲线 ,
, 有公共点,且在该点处的切线相同.(I)用
有公共点,且在该点处的切线相同.(I)用 表示
表示 ;(II)求证:
;(II)求证: (
( ).
).(Ⅰ)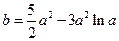 (Ⅱ)略
(Ⅱ)略
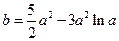 (Ⅱ)略
(Ⅱ)略(Ⅰ)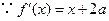 ,
,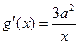 ,设
,设 与
与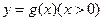 在公共点
在公共点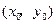 处的切线相同,由题意
处的切线相同,由题意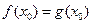 ,
,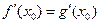

即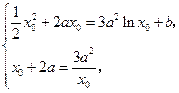 由
由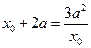 得:
得: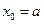 ,或
,或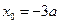 (舍去)
(舍去)
即有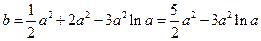

(Ⅱ)设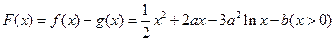 ,
,
则
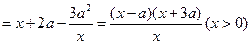

x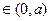 时
时 <0,x
<0,x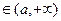
 >0,∴
>0,∴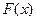 在
在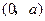 为减函数,在
为减函数,在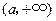 为增函数,于是函数
为增函数,于是函数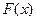 在
在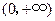 上的最小值是:F(a)=f(a)-g(a)=0,故当
上的最小值是:F(a)=f(a)-g(a)=0,故当 时,有
时,有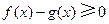 ,所以,当
,所以,当 时,
时,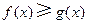

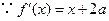 ,
,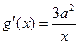 ,设
,设 与
与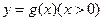 在公共点
在公共点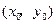 处的切线相同,由题意
处的切线相同,由题意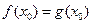 ,
,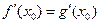

即
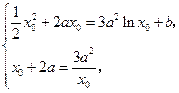 由
由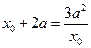 得:
得: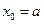 ,或
,或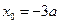 (舍去)
(舍去)
即有
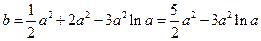

(Ⅱ)设
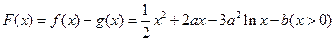 ,
,则

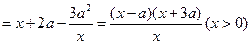

x
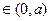 时
时 <0,x
<0,x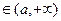
 >0,∴
>0,∴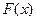 在
在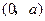 为减函数,在
为减函数,在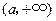 为增函数,于是函数
为增函数,于是函数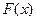 在
在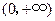 上的最小值是:F(a)=f(a)-g(a)=0,故当
上的最小值是:F(a)=f(a)-g(a)=0,故当 时,有
时,有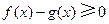 ,所以,当
,所以,当 时,
时,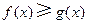


练习册系列答案
相关题目
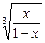 .
.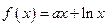 ,
,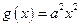 .
.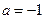 时,求函数
时,求函数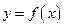 图象上的点到直线
图象上的点到直线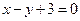 距离的最小值;
距离的最小值;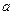 ,使
,使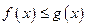 对一切正实数
对一切正实数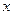 都成立?若存在,求出
都成立?若存在,求出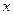 的三次函数
的三次函数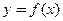 的两个极值点为P、Q,其中P为原点,Q在曲线
的两个极值点为P、Q,其中P为原点,Q在曲线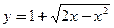 上,则曲线
上,则曲线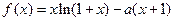 ,其中
,其中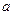 为常数.
为常数.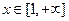 时,
时,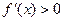 恒成立,求
恒成立,求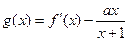 的单调区间.
的单调区间.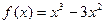 ,给出下列四个命题:①
,给出下列四个命题:①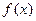 是增函数,无极值;②
是增函数,无极值;②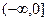 及
及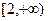 上是增函数;④
上是增函数;④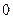 ,极小值
,极小值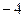 ;其中正确命题的个数为( )
;其中正确命题的个数为( )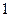
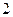

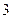
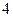
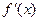 是
是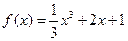 的导函数,则
的导函数,则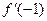 的值是 .
的值是 .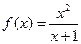 的导数。
的导数。