题目内容
已知双曲线E的中心为原点,F(3,0)是E的焦点,过F的直线l与E相交于A、B两点,且AB的中点为N(-12,-15),则E的方程为( )
(A)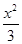 -
- =1 (B)
=1 (B) -
-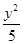 =1
=1
(C) -
- =1 (D)
=1 (D)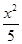 -
- =1
=1
(A)
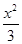 -
- =1 (B)
=1 (B) -
-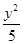 =1
=1(C)
 -
- =1 (D)
=1 (D)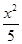 -
- =1
=1B
∵kAB=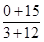 =1,
=1,
∴直线AB的方程为y=x-3.
由于双曲线的焦点为F(3,0),
∴c=3,c2=9.
设双曲线的标准方程为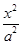 -
-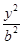 =1(a>0,b>0),
=1(a>0,b>0),
则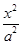 -
-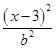 =1.整理,得
=1.整理,得
(b2-a2)x2+6a2x-9a2-a2b2=0.
设A(x1,y1),B(x2,y2),
则x1+x2=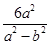 =2×(-12),
=2×(-12),
∴a2=-4a2+4b2,∴5a2=4b2.
又a2+b2=9,
∴a2=4,b2=5.
∴双曲线E的方程为 -
-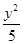 =1.故选B.
=1.故选B.
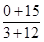 =1,
=1,∴直线AB的方程为y=x-3.
由于双曲线的焦点为F(3,0),
∴c=3,c2=9.
设双曲线的标准方程为
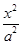 -
-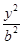 =1(a>0,b>0),
=1(a>0,b>0),则
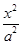 -
-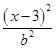 =1.整理,得
=1.整理,得(b2-a2)x2+6a2x-9a2-a2b2=0.
设A(x1,y1),B(x2,y2),
则x1+x2=
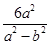 =2×(-12),
=2×(-12),∴a2=-4a2+4b2,∴5a2=4b2.
又a2+b2=9,
∴a2=4,b2=5.
∴双曲线E的方程为
 -
-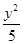 =1.故选B.
=1.故选B.
练习册系列答案
相关题目
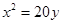 的焦点重合,且其渐近线的方程为
的焦点重合,且其渐近线的方程为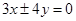 ,则该双曲线的标准方程为
,则该双曲线的标准方程为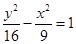
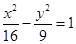
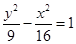
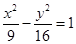
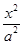 -
- =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为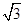 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )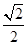 x
x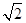 x
x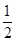 x
x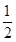
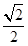
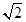
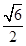 的是( )
的是( )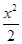 -
-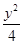 =1
=1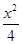 -
- =1
=1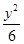 =1
=1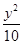 =1
=1 (a>0,b>0)称为黄金双曲线.如图,
(a>0,b>0)称为黄金双曲线.如图,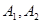 是双曲线的实轴顶点,
是双曲线的实轴顶点,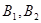 是虚轴的顶点,
是虚轴的顶点,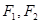 是左右焦点,
是左右焦点,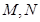 在双曲线上且过右焦点
在双曲线上且过右焦点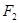 ,并且
,并且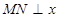 轴,给出以下几个说法:
轴,给出以下几个说法: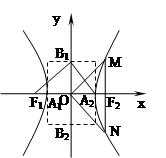
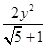 =1是黄金双曲线;
=1是黄金双曲线;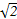 x,那么它的两条准线间的距离是( )
x,那么它的两条准线间的距离是( )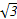
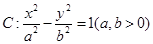 的左、右焦点分别为
的左、右焦点分别为
 ,过
,过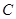 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为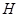 ,若
,若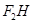 的中点
的中点 在双曲线
在双曲线