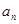题目内容
如图,在凸四边形ABCD中,C,D为定点,CD=
,A,B为动点,满足AB=BC=DA=1.
(Ⅰ)写出cosC与cosA的关系式;
(Ⅱ)设△BCD和△ABD的面积分别为S和T,求S2+T2的最大值.
| 3 |
(Ⅰ)写出cosC与cosA的关系式;
(Ⅱ)设△BCD和△ABD的面积分别为S和T,求S2+T2的最大值.

(Ⅰ)连接BD,
∵CD=
,AB=BC=DA=1,
∴在△BCD中,利用余弦定理得:BD2=BC2+CD2-2BC•CDcosC=4-2
cosC;
在△ABD中,BD2=2-2cosA,
∴4-2
cosC=2-2cosA,
则cosA=
cosC-1;
(Ⅱ)S=
BC•CD•sinC=
sinC,T=
AB•ADsinA=
sinA,
∵cosA=
cosC-1,
∴S2+T2=
sin2C+
sin2A=
(1-cos2C)+
(1-cos2A)=-
cos2C+
cosC+
=-
(cosC-
)2+
,
∵cosA=
cosC-1>0,即cosC>
,
∴C∈(30°,90°),∴cosC∈(0,
),
则当cosC=
时,S2+T2有最大值
.
∵CD=
| 3 |
∴在△BCD中,利用余弦定理得:BD2=BC2+CD2-2BC•CDcosC=4-2
| 3 |
在△ABD中,BD2=2-2cosA,
∴4-2
| 3 |
则cosA=
| 3 |
(Ⅱ)S=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵cosA=
| 3 |
∴S2+T2=
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| ||
| 6 |
| 7 |
| 8 |
∵cosA=
| 3 |
| ||
| 2 |
∴C∈(30°,90°),∴cosC∈(0,
| ||
| 2 |
则当cosC=
| ||
| 6 |
| 7 |
| 8 |

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
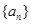 为等差数列,且
为等差数列,且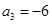 ,
,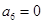 .
.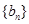 满足
满足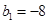 ,
,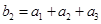 ,求
,求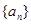 的前
的前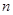 项和
项和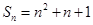 ,
,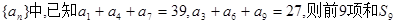 的值为( )
的值为( ) 前项和为
前项和为 ,且点
,且点 在
在 图像上,求
图像上,求