题目内容
9.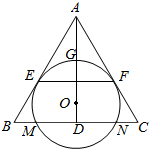 如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;
(2)若AG等于⊙O的半径,且AE=MN=2$\sqrt{3}$,求四边形EBCF的面积.
分析 (1)通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F,利用相似的性质即得结论;
(2)通过(1)知AD是EF的垂直平分线,连结OE、OM,则OE⊥AE,利用S△ABC-S△AEF计算即可.
解答 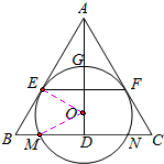 (1)证明:∵△ABC为等腰三角形,AD⊥BC,
(1)证明:∵△ABC为等腰三角形,AD⊥BC,
∴AD是∠CAB的角平分线,
又∵圆O分别与AB、AC相切于点E、F,
∴AE=AF,∴AD⊥EF,
∴EF∥BC;
(2)解:由(1)知AE=AF,AD⊥EF,∴AD是EF的垂直平分线,
又∵EF为圆O的弦,∴O在AD上,
连结OE、OM,则OE⊥AE,
由AG等于圆O的半径可得AO=2OE,
∴∠OAE=30°,∴△ABC与△AEF都是等边三角形,
∵AE=2$\sqrt{3}$,∴AO=4,OE=2,
∵OM=OE=2,DM=$\frac{1}{2}$MN=$\sqrt{3}$,∴OD=1,
∴AD=5,AB=$\frac{10\sqrt{3}}{3}$,
∴四边形EBCF的面积为$\frac{1}{2}×$$(\frac{10\sqrt{3}}{3})^{2}$×$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$×$(2\sqrt{3})^{2}$×$\frac{\sqrt{3}}{2}$=$\frac{16\sqrt{3}}{3}$.
点评 本题考查空间中线与线之间的位置关系,考查四边形面积的计算,注意解题方法的积累,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
20.某校老年、中年和青年教师的人数见如表,采用分层插样的方法调查教师的身体状况,在抽取的样本中,青年教师有320人,则该样本的老年教师人数为( )
| 类别 | 人数 |
| 老年教师 | 900 |
| 中年教师 | 1800 |
| 青年教师 | 1600 |
| 合计 | 4300 |
| A. | 90 | B. | 100 | C. | 180 | D. | 300 |
17.已知等比数列{an}满足a1=3,a1+a3+a5=21,则a3+a5+a7=( )
| A. | 21 | B. | 42 | C. | 63 | D. | 84 |
19.某同学将“五点法”画函数f(x)=Asin(wx+φ)(w>0,|φ|<$\frac{π}{2}$)在某一个时期内的图象时,列表并填入部分数据,如下表:
(1)请将上述数据补充完整,填写在答题卡上相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平移$\frac{π}{6}$个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.
| wx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin(wx+φ) | 0 | 5 | -5 | 0 |
(2)将y=f(x)图象上所有点向左平移$\frac{π}{6}$个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.