题目内容
11．已知等比数列{an}满足a1=$\frac{1}{4}$，a3a5=4（a4-1），则a2=（ ）| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{8}$ |
分析 利用等比数列的通项公式即可得出．
解答 解：设等比数列{an}的公比为q，
∵${a_1}=\frac{1}{4}$，a3a5=4（a4-1），
∴$（\frac{1}{4}）^{2}×{q}^{6}$=4$（\frac{1}{4}{q}^{3}-1）$，
化为q3=8，解得q=2
则a2=$\frac{1}{4}×2$=$\frac{1}{2}$．
故选：C．
点评 本题考查了等比数列的通项公式，属于基础题．
练习册系列答案
相关题目
2．（x2+x+y）5的展开式中，x5y2的系数为（ ）
| A． | 10 | B． | 20 | C． | 30 | D． | 60 |
19．某同学将“五点法”画函数f（x）=Asin（wx+φ）（w＞0，|φ|＜$\frac{π}{2}$）在某一个时期内的图象时，列表并填入部分数据，如下表：
（1）请将上述数据补充完整，填写在答题卡上相应位置，并直接写出函数f（x）的解析式；
（2）将y=f（x）图象上所有点向左平移$\frac{π}{6}$个单位长度，得到y=g（x）图象，求y=g（x）的图象离原点O最近的对称中心．
| wx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin（wx+φ） | 0 | 5 | -5 | 0 |
（2）将y=f（x）图象上所有点向左平移$\frac{π}{6}$个单位长度，得到y=g（x）图象，求y=g（x）的图象离原点O最近的对称中心．
6．已知集合A={x|-1＜x＜2}，B={x|0＜x＜3}，则A∪B=（ ）
| A． | （-1，3） | B． | （-1，0） | C． | （0，2） | D． | （2，3） |
16．某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表
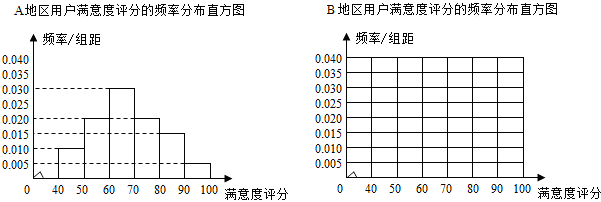
B地区用户满意度评分的频数分布表
（1）做出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）
（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：
估计哪个地区用户的满意度等级为不满意的概率大？说明理由．
B地区用户满意度评分的频数分布表
| 满意度评分分组 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
| 频数 | 2 | 8 | 14 | 10 | 6 |
（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
3．设x∈R，则“|x-2|＜1”是“x2+x-2＞0”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
20．
如图，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′-CD-B的平面角为α，则（ ）
如图，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′-CD-B的平面角为α，则（ ）| A． | ∠A′DB≤α | B． | ∠A′DB≥α | C． | ∠A′CB≤α | D． | ∠A′CB≥α |
某山区外围有两条相互垂直的直线型公路，为进一步改善山区的交通现状，计划修建一条连接两条公路和山区边界的直线型公路，记两条相互垂直的公路为l1，l2，山区边界曲线为C，计划修建的公路为l，如图所示，M，N为C的两个端点，测得点M到l1，l2的距离分别为5千米和40千米，点N到l1，l2的距离分别为20千米和2.5千米，以l2，l1在的直线分别为x，y轴，建立平面直角坐标系xOy，假设曲线C符合函数y=$\frac{a}{{x}^{2}+b}$（其中a，b为常数）模型．