题目内容
【题目】已知函数f(x)= ![]() .
.
( I)判断f(x)的奇偶性;
( II)求证:f(x)+f( ![]() )为定值;
)为定值;
(III)求 ![]() +
+ ![]() +
+ ![]() +f(1)+f(2015)+f(2016)+f(2017)的值.
+f(1)+f(2015)+f(2016)+f(2017)的值.
【答案】解:(I)∵函数f(x)= ![]() .
.
∴函数f(x)= ![]() 的定义域R,定义域关于原点对称.
的定义域R,定义域关于原点对称.
又 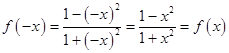 ,
,
∴f(x)是偶函数.…(4分)
证明:(Ⅱ)∵ 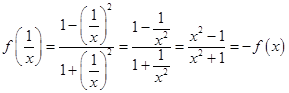 ,
,
∴ ![]() 为定值.
为定值.
解:(Ⅲ)由(II)知 ![]() ,
,![]() +
+ ![]() +
+ ![]() +f(1)+f(2015)+f(2016)+f(2017)
+f(1)+f(2015)+f(2016)+f(2017)
= ![]()
=0+f(1)=0.
【解析】(I)先求出函数f(x)的定义域关于原点对称,再由f(﹣x)=f(x),得到f(x)是偶函数.(Ⅱ)推导出f( ![]() )=﹣f(x),由此能证明
)=﹣f(x),由此能证明 ![]() 为定值.(Ⅲ)由
为定值.(Ⅲ)由 ![]() ,能求出
,能求出 ![]() +
+ ![]() +
+ ![]() +f(1)+f(2015)+f(2016)+f(2017)的值.
+f(1)+f(2015)+f(2016)+f(2017)的值.
【考点精析】解答此题的关键在于理解函数的奇偶性的相关知识,掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称,以及对函数的值的理解,了解函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法.

练习册系列答案
相关题目