题目内容
【题目】已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球![]() 个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是
个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .求在区间
.求在区间![]() 内任取2个实数
内任取2个实数![]() ,
,![]() ,求事件“
,求事件“![]() 恒成立”的概率.
恒成立”的概率.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据古典概型概率计算公式列方程,解方程求得![]() 的值.
的值.
(Ⅱ)先求得![]() 的最大值,由此得到“
的最大值,由此得到“![]() 恒成立”,根据几何概型概率计算公式,计算出所求概率.
恒成立”,根据几何概型概率计算公式,计算出所求概率.
(Ⅰ)根据从袋子随机抽取1个小球,取到标号为2的小球的概率是![]() ,可得
,可得![]() .
.
解得![]()
(Ⅱ)依题意可知![]() 的最大值为
的最大值为![]() .
.
设![]() 恒成立为事件
恒成立为事件![]() ,则事件
,则事件![]() 等价于“
等价于“![]() 恒成立”.
恒成立”.
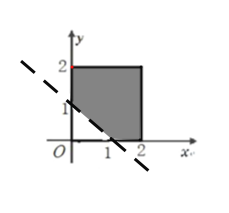
![]() 可以看成平面中的点,则全部结果所构成的区域为
可以看成平面中的点,则全部结果所构成的区域为![]() ,
,
![]() 表示直线
表示直线![]() 右上方部分.
右上方部分.
所以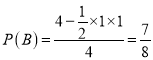 .
.

练习册系列答案
相关题目
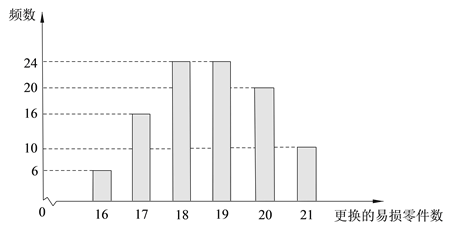
【题目】某高校在2015年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| a |
|
第3组 |
| 30 | b |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
合计 | 100 |
| |
![]() Ⅰ
Ⅰ![]() 求出频率分布表中a,b的值,再在答题纸上完成频率分布直方图;
求出频率分布表中a,b的值,再在答题纸上完成频率分布直方图;
![]() Ⅱ
Ⅱ![]() 根据样本频率分布直方图估计样本成绩的中位数;
根据样本频率分布直方图估计样本成绩的中位数;
![]() Ⅲ
Ⅲ![]() 高校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,再从6名学生中随机抽取2名学生由A考官进行面试,求第4组至少有一名学生被考官A面试的概率.
高校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,再从6名学生中随机抽取2名学生由A考官进行面试,求第4组至少有一名学生被考官A面试的概率.