题目内容
8.已知集合An={(a1,a2,…an)|aj=0或1,j=1,2,…,n(n≥2)},对于U,V∈An,d(U,V)表示U和V中相对应的元素不同的个数,若给定U∈An,则所有的d(U,V)和为n2n-1.分析 易知An中共有2n个元素,分别记为vk(k=1,2,3,…,2n,v=(b1,b2,b3,…bn)bi=0的vk共有2n-1个,bi=1的vk共有2n-1个然后求和即可.
解答 解:易知An中共有2n个元素,分别记为vk(k=1,2,3,…,2n),
V=(b1,b2,b3,…,bn)
∵bi=0的vk共有2n-1个,bi=1的vk共有2n-1个.
∴d(U,V)=2n-1(|a1-0|+|a1-1|+|a2-0|+a2-1|+|a3-0|+|a3-1|+…+|an-0|+|an-1|)=n×2n-1
∴d(U,V)=n×2n-1.
故答案为:n×2n-1
点评 此题是个难题.本题是综合考查集合推理综合的应用,这道题目的难点主要出现在读题上,需要仔细分析,以找出解题的突破点.题目所给的条件其实包含两个定义,第一个是关于Sn的,其实Sn中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1,第二个定义d(U,V).

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
18.下列命题中正确命题的个数是( )
①对于命题P:存在x∈R,使得x2+x-1<0,则﹁P:任意x∈R,均有x2+x-1>0
②命题“若x=y,则sinx=siny”的逆否命题为真命题
③“m=-1”是“直线l1:mx+(2m-1)y+1=0与直线l2:3x+my+3=0垂直”的充要条件.
①对于命题P:存在x∈R,使得x2+x-1<0,则﹁P:任意x∈R,均有x2+x-1>0
②命题“若x=y,则sinx=siny”的逆否命题为真命题
③“m=-1”是“直线l1:mx+(2m-1)y+1=0与直线l2:3x+my+3=0垂直”的充要条件.
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
19.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,且|$\overrightarrow{b}$|=2,$\overrightarrow{b}$$•(2\overrightarrow{a}-\overrightarrow{b})$=0,则|$\overrightarrow{a}$|的最小值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
16.已知α∈(π,2π),且cosα+sinα=$\frac{1}{5}$,则tanα=( )
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
14.已知命题p:若a>b,则a2>b2;q:“x≤1”是“x2+2x-3≤0”的必要不充分条件.则下列命题是真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧¬q |
15.已知一几何体的三视图如图所示,则该几何体的体积是( )
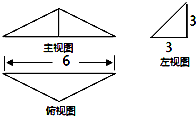

| A. | 6 | B. | 9 | C. | 12 | D. | 18 |