题目内容
12.下列函数:①f(x)=2x-1;②f(x)=lnx+2x-6;③f(x)=x2+2x+1;④f(x)=${(\frac{1}{2})}^{x}$-1;⑤f(x)=x3+2.不能用二分法求零点的是③.分析 根据用二分法求方程的近似解的方法,函数必须是连续函数,且函数在零点两侧的函数值异号,由此检验各个选项中的函数函数,作出判断.
解答 解::①f(x)=2x-1有唯一零点,且函数在零点两侧的函数值异号,故可用二分法求出零点.
②f(x)=lnx+2x-6是连续函数,且f(2)<0,f(3)>0,故可用二分法求出零点;
③f(x)=x2+2x+1的零点为x=-1,函数在x=-1两侧的函数值符号相同,不异号,故此函数不能用二分法求零点.
④f(x)=${(\frac{1}{2})}^{x}$-1唯一零点是x=0,且函数在零点两侧的函数值异号,故可用二分法求出零点.
⑤f(x)=x3+2唯一零点是x=-$\root{3}{2}$,且函数在零点两侧的函数值异号,故可用二分法求出零点,
故答案为:③.
点评 本题主要考查用二分法求方程的近似解,注意用二分法求方程的近似解的条件,属于基础题.

练习册系列答案
相关题目
17.若输出的i=5,则k的最小正整数值为( )
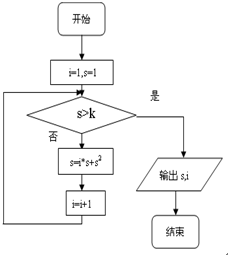

| A. | 88 | B. | 89 | C. | 8095 | D. | 8096 |
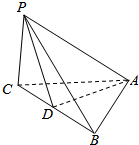 如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.
如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.