题目内容
如图,已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点 、
、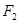 在x轴上,离心率
在x轴上,离心率
(1)求椭圆E的方程;
(2)求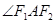 的角平分线所在直线
的角平分线所在直线 的方程.
的方程.
 、
、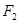 在x轴上,离心率
在x轴上,离心率
(1)求椭圆E的方程;
(2)求
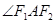 的角平分线所在直线
的角平分线所在直线 的方程.
的方程.
(1)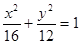 (2)
(2)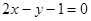
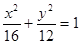 (2)
(2)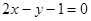
(1)根据点A(2,3)在椭圆上和e可以建立关于a,b,c的方程,解出a,b的值.
(2)根据到角公式求解即可
(2)根据到角公式求解即可

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
题目内容
 、
、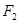 在x轴上,离心率
在x轴上,离心率
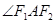 的角平分线所在直线
的角平分线所在直线 的方程.
的方程.
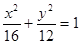 (2)
(2)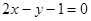

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案