题目内容
直线l1:(3-m)x+(m-1)y-1=0和l2:(m-1)x+(1-2m)y+1=0互相垂直,那么m等于( )
| A.1 | B.
| C.1或
| D.3或4 |
当m=1时,直线l1的斜率不存在,l2的斜率等于0,两直线互相垂直,故m=1满足条件.
当m=
时,直线l1的斜率不等于0,l2的斜率不存在,两直线不互相垂直,故m=1不满足条件.
当m≠1且m≠
时,根据两直线垂直,斜率之积等于-1得:
×
=-1,
解得 m=
或m=1,综上,m=1或 m=
,故选 C.
当m=
| 1 |
| 2 |
当m≠1且m≠
| 1 |
| 2 |
| m-3 |
| m-1 |
| m-1 |
| 2m-1 |
解得 m=
| 4 |
| 3 |
| 4 |
| 3 |

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 两点,且在
两点,且在 轴上截得的线段长为
轴上截得的线段长为 ,半径小于5.(1)求直线
,半径小于5.(1)求直线 与圆C的方程;(2)若直线
与圆C的方程;(2)若直线 ,直线
,直线 与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线
与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线
 与
与 的交点在第一象限内,则
的交点在第一象限内,则 的取值范围是( )
的取值范围是( )



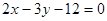 与坐标轴围成的三角形的面积为 .
与坐标轴围成的三角形的面积为 .