题目内容
已知圆C经过 两点,且在
两点,且在 轴上截得的线段长为
轴上截得的线段长为 ,半径小于5.(1)求直线
,半径小于5.(1)求直线 与圆C的方程;(2)若直线
与圆C的方程;(2)若直线 ,直线
,直线 与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线
与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线 的方程.
的方程.
 两点,且在
两点,且在 轴上截得的线段长为
轴上截得的线段长为 ,半径小于5.(1)求直线
,半径小于5.(1)求直线 与圆C的方程;(2)若直线
与圆C的方程;(2)若直线 ,直线
,直线 与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线
与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线 的方程.
的方程. (1)直线PQ: ,圆C方程:
,圆C方程:
(2)直线 或
或 .
.
 ,圆C方程:
,圆C方程:
(2)直线
 或
或 .
.试题分析:(1)根据直线方程的点斜式求解所求的直线方程是解决本题的关键,根据待定系数法设出圆心坐标和半径,寻找未知数之间的关系是求圆的方程的关键,注意弦长问题的处理方法;
(2)利用直线的平行关系设出直线的方程,利用设而不求的思想得到关于所求直线方程中未知数的方程,通过方程思想确定出所求的方程,注意对所求的结果进行验证和取舍.
试题解析:(1)直线PQ的方程为
 即直线PQ的方程为x+y-2=0,
即直线PQ的方程为x+y-2=0,C在PQ的中垂线
 即y=x-1上,
即y=x-1上,设C(n,n-1),则r2=|CQ|2=(n+1)2+(n-4)2,
由题意,有
 ∴n2+12=2n2-6n+17,
∴n2+12=2n2-6n+17,∴n=1或5(舍去),r2=13或37(舍去),
∴圆C的方程为
 .
.(2)设直线l的方程为x+y+m=0,由
 ,消去y得2x2+(2m-2)x+m2-12=0,
,消去y得2x2+(2m-2)x+m2-12=0,设A(x1,y1),B(x2,y2),则x1+x2=1-m,x1x2=

又∵以AB为直径的圆经过坐标原点
 ∠AOB=90°,∴x1x2+y1y2=0
∠AOB=90°,∴x1x2+y1y2=0∴
 ,将韦达定理的结果代入并整理化间得m2+m-12=0,
,将韦达定理的结果代入并整理化间得m2+m-12=0,∴m=3或-4(均满足△>0),
∴l的方程为x+y+3=0或x+y-4=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在x轴和y轴上的截距相等,则a=
在x轴和y轴上的截距相等,则a=
 +
+ =1与x,y轴交点的中点的轨迹方程是________.
=1与x,y轴交点的中点的轨迹方程是________.
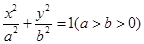 上的点到椭圆右焦点
上的点到椭圆右焦点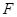 的最大距离为
的最大距离为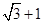 ,离心率
,离心率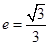 ,直线
,直线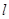 过点
过点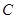 交于
交于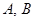 两点.
两点.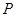 ,使得当
,使得当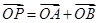 成立?若存在,求出所有点
成立?若存在,求出所有点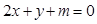 和
和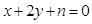 的位置关系是( )
的位置关系是( )