题目内容
9.解方程组:$\left\{\begin{array}{l}{3(x+y)-4(x-y)=4}\\{\frac{x+y}{2}+\frac{x-y}{6}=1}\end{array}\right.$.分析 利用换元法,设设x+y=m,x-y=n,得到关于m,n的方程组,求出吗,n的值,再得到关于x,y的方程组,解得即可.
解答 解:设x+y=m,x-y=n,
则$\left\{\begin{array}{l}{3m-4n=4}\\{\frac{m}{2}+\frac{n}{6}=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{28}{15}}\\{n=\frac{2}{5}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x+y=\frac{28}{15}}\\{x-y=\frac{2}{5}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{17}{15}}\\{y=\frac{11}{15}}\end{array}\right.$.
点评 本题考查了方程组的解法,关键是换元,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.函数f(x)=$\frac{{\sqrt{16-{x^2}}}}{{|{x+5}|+|{x-4}|}}$为( )
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |
20.若-$\frac{π}{2}$<α<β<$\frac{π}{2}$,则α-β的取值范围是( )
| A. | (-π,π) | B. | (0,π) | C. | (-π,0) | D. | {0} |
14.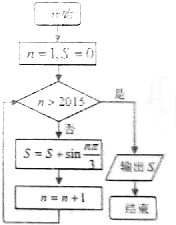 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )
 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
18.函数f(x)=$\sqrt{x-1}$的定义域是( )
| A. | [1,+∞) | B. | (1,+∞) | C. | (0,1) | D. | [0,1] |
19.已知△ABC中,cosA=$\frac{2\sqrt{5}}{5}$,cosB=$\frac{3\sqrt{10}}{10}$,则内角C等于( )
| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |