题目内容
11．在平面直角坐标系xOy中，点A（-1，-2），B（2，3）．（1）求向量$\overrightarrow{AB}$；
（2）若向量$\overrightarrow{a}∥\overrightarrow{AB}$，且$\overrightarrow{a}$=（1，k），求k．
分析 （1）根据平面向量的坐标表示，写出向量$\overrightarrow{AB}$即可；
（2）由两向量平行的坐标表示，列出方程，求出k的值．
解答 解：（1）平面直角坐标系xOy中，点A（-1，-2），B（2，3）．
∴向量$\overrightarrow{AB}$=（2+1，3+2）=（3，5）；
（2）∵向量$\overrightarrow{a}∥\overrightarrow{AB}$，$\overrightarrow{a}$=（1，k），
∴3k-5×1=0，
解得k=$\frac{5}{3}$．
点评 本题考查了平面向量的坐标表示与应用问题，是基础题目．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
19．已知△ABC中，cosA=$\frac{2\sqrt{5}}{5}$，cosB=$\frac{3\sqrt{10}}{10}$，则内角C等于（ ）
| A． | $\frac{3π}{4}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
6．圆（x-1）2+（y-2）2=1的圆心坐标是（ ）
| A． | （1，2） | B． | （-1，-2） | C． | （2，1） | D． | （-2，-1） |
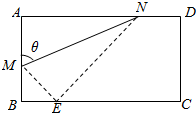如图，折叠矩形纸片ABCD，使A点落在边BC上的E处，折痕的两端点M、N分别在线段AB和AD上（不与端点重合）．已知AB=2，BC=$\frac{{4\sqrt{3}}}{3}$，设∠AMN=θ．