题目内容
10．若函数f（x）=2sin（ωx）（ω＞0）的最小正周期为$\frac{π}{2}$，则ω=4．分析 由三角函数的周期性及其求法可得T=$\frac{π}{2}$=$\frac{2π}{ω}$，即可解得ω的值．
解答 解：由三角函数的周期性及其求法可得：T=$\frac{π}{2}$=$\frac{2π}{ω}$，
解得：ω=4．
故答案为：4．
点评 本题主要考查了三角函数的周期性及其求法，属于基本知识的考查．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
20．若-$\frac{π}{2}$＜α＜β＜$\frac{π}{2}$，则α-β的取值范围是（ ）
| A． | （-π，π） | B． | （0，π） | C． | （-π，0） | D． | {0} |
18．函数f（x）=$\sqrt{x-1}$的定义域是（ ）
| A． | [1，+∞） | B． | （1，+∞） | C． | （0，1） | D． | [0，1] |
5．函数f（x）=sin2x与函数g（x）=2x的图象的交点的个数是（ ）
| A． | 1 | B． | 3 | C． | 5 | D． | 7 |
19．已知△ABC中，cosA=$\frac{2\sqrt{5}}{5}$，cosB=$\frac{3\sqrt{10}}{10}$，则内角C等于（ ）
| A． | $\frac{3π}{4}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
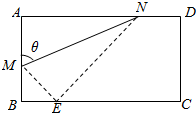如图，折叠矩形纸片ABCD，使A点落在边BC上的E处，折痕的两端点M、N分别在线段AB和AD上（不与端点重合）．已知AB=2，BC=$\frac{{4\sqrt{3}}}{3}$，设∠AMN=θ．