题目内容
4.已知平面内两点A(2acos2$\frac{ωx+φ}{2}$,1),B(1,$\sqrt{3}$asin(ωx+φ)-a),(a≠0,ω>0,0<φ<$\frac{π}{2}$),设函数f(x)=$\overrightarrow{OA}$•$\overrightarrow{OB}$,若f(x)的图象相邻两最高点的距离为π,且有一个对称中心为($\frac{π}{3}$,0).(1)求ω和φ的值;
(2)求f(x)的单调递增区间;
(3)若a>0,试讨论k为何值时,方程f(x)-k=0(x∈[0,a])有解.
分析 (1)首先由数量积公式求出函数的解析式,然后化简为最简形式,利用f(x)的图象相邻两最高点的距离为π,得到其周期为2π,求出ω;利用有一个对称中心为($\frac{π}{3}$,0)求出φ;
(2)利用正弦函数的单调递增区间,求f(x)的单调递增区间;
(3)讨论a,分别求出最大值和最小值,求出方程f(x)-k=0(x∈[0,a])有解的k的范围.
解答 解:(1)$f(x)=\overrightarrow{OA}•\overrightarrow{OB}=2a{cos^2}\frac{ωx+φ}{2}+\sqrt{3}asin(ωx+φ)-a$…(1分)
=$acos(ωx+φ)+\sqrt{3}asin(ωx+φ)$…(2分)
=$2asin(ωx+φ+\frac{π}{6})$…(3分)
∵f(x)的图象相邻两最高点的距离为π,
∴$\frac{2π}{ω}=π$,ω=2…(4分)
又其图象的一个对称中心为$(\frac{π}{3},0)$,故$2×\frac{π}{3}+φ+\frac{π}{6}=kπ(k∈Z)$,∴$φ=kπ-\frac{5π}{6}(k∈Z)$,由$0<φ<\frac{π}{2}$得$φ=\frac{π}{6}$…(5分)
(2)由(1)知$f(x)=2asin(2x+\frac{π}{3})$
当a>0时,由$-\frac{π}{2}+2kπ≤2x+\frac{π}{3}≤\frac{π}{2}+2kπ$,得f(x)单调增区间为$[-\frac{5π}{12}+kπ,\frac{π}{12}+kπ]$,k∈Z…(7分)
当a<0时,由$\frac{π}{2}+2kπ≤2x+\frac{π}{3}≤\frac{3π}{2}+2kπ$,得f(x)单调增区间为$[\frac{π}{12}+kπ,\frac{7π}{12}+kπ]$,k∈Z…(9分)
(3)当$0<a<\frac{π}{12}$时,由x∈[0,a]得$f{(x)_{max}}=f(a)=2asin(2a+\frac{π}{3})$,$f{(x)_{min}}=f(0)=\sqrt{3}a$…(10分)
当$\frac{π}{12}≤a≤\frac{π}{6}$时,由x∈[0,a]得$f{(x)_{max}}=f(\frac{π}{12})=2a$,$f{(x)_{min}}=f(0)=\sqrt{3}a$…(11分)
当$\frac{π}{6}<a<\frac{7π}{12}$时,由x∈[0,a]得$f{(x)_{max}}=f(\frac{π}{12})=2a$,$f{(x)_{min}}=f(a)=2asin(2a+\frac{π}{3})$…(12分)
当$a≥\frac{7π}{12}$时,由x∈[0,a]得$f{(x)_{max}}=f(\frac{π}{12})=2a$,$f{(x)_{min}}=f(\frac{7π}{12})=-2a$…(13分)
综上所述:
要使方程f(x)-k=0(x∈[0,a])有解,当$0<a<\frac{π}{12}$时,$\sqrt{3}a≤k≤2asin(2a+\frac{π}{3})$;
当$\frac{π}{12}≤a≤\frac{π}{6}$时,$\sqrt{3}a≤k≤2a$;
当$\frac{π}{6}<a<\frac{7π}{12}$时,$2asin(2a+\frac{π}{3})≤k≤2a$;
当$a≥\frac{7π}{12}$时,-2a≤k≤2a…(14分)
点评 本题考查了平面向量的数量积、三角函数的化简、三角函数性质运用;属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案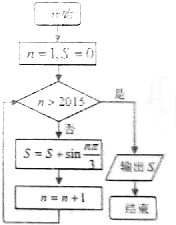 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不能确定 |