题目内容
已知椭圆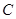 :
: 的左、右顶点分别为
的左、右顶点分别为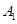 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 ,离心率是
,离心率是 .
.
(Ⅰ)求椭圆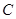 的方程;
的方程;
(Ⅱ)若点 是椭圆
是椭圆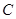 上异于
上异于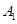 ,
, 的任意一点,直线
的任意一点,直线 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 (
( 为椭圆
为椭圆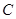 的右焦点).
的右焦点).
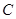 :
: 的左、右顶点分别为
的左、右顶点分别为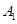 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 ,离心率是
,离心率是 .
.(Ⅰ)求椭圆
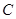 的方程;
的方程;(Ⅱ)若点
 是椭圆
是椭圆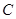 上异于
上异于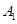 ,
, 的任意一点,直线
的任意一点,直线 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 (
( 为椭圆
为椭圆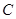 的右焦点).
的右焦点).(Ⅰ)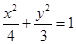 .(Ⅱ)证明:见解析。
.(Ⅱ)证明:见解析。
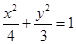 .(Ⅱ)证明:见解析。
.(Ⅱ)证明:见解析。(I)由题意可得 ,再根据
,再根据 ,求出a,b的值.
,求出a,b的值.
(II) 以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 本质是证明:
本质是证明: 且
且 .然后利用坐标表示出来,再根据条件把M、N的坐标求出来,证明即可.
.然后利用坐标表示出来,再根据条件把M、N的坐标求出来,证明即可.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑.
(Ⅰ)解:由已知
解得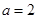 ,
,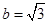 . …………4分故所求椭圆方程为
. …………4分故所求椭圆方程为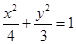 .
.
(Ⅱ)证明:由(Ⅰ)知 ,
, ,设椭圆右焦点
,设椭圆右焦点 .设
.设 ,则
,则 .于是直线
.于是直线 方程为
方程为 ,令
,令 ,得
,得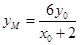 ;
;
所以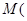
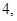

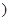 ,同理
,同理
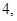
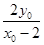
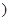 .
.
所以
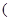
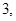

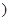 ,
,
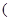
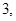
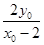
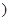 .
.
所以
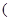
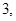

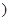

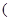
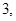
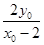
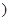

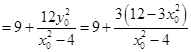
 .
.
所以 ,点
,点 在以
在以 为直径的圆上.
为直径的圆上.
设 的中点为
的中点为 ,则
,则
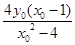
 .
.
又

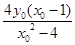
 ,
,
所以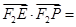

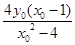
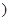

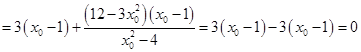 .
.
所以 .…………12分
.…………12分
因为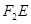 是以
是以 为直径的圆的半径,
为直径的圆的半径, 为圆心,
为圆心, ,故以
,故以 为直径的圆与直线
为直径的圆与直线 相切于右焦点.
相切于右焦点.
 ,再根据
,再根据 ,求出a,b的值.
,求出a,b的值.(II) 以
 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 本质是证明:
本质是证明: 且
且 .然后利用坐标表示出来,再根据条件把M、N的坐标求出来,证明即可.
.然后利用坐标表示出来,再根据条件把M、N的坐标求出来,证明即可.请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑.
(Ⅰ)解:由已知

解得
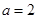 ,
,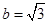 . …………4分故所求椭圆方程为
. …………4分故所求椭圆方程为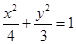 .
.(Ⅱ)证明:由(Ⅰ)知
 ,
, ,设椭圆右焦点
,设椭圆右焦点 .设
.设 ,则
,则 .于是直线
.于是直线 方程为
方程为 ,令
,令 ,得
,得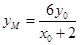 ;
;所以
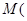
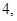

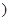 ,同理
,同理
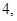
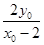
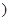 .
.所以

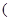
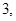

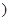 ,
,
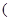
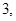
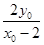
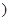 .
.所以

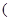
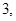

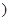

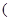
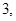
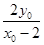
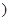

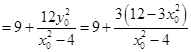
 .
.所以
 ,点
,点 在以
在以 为直径的圆上.
为直径的圆上.设
 的中点为
的中点为 ,则
,则
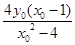
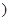 .
.又


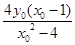
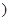 ,
,
所以
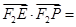

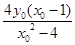
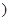

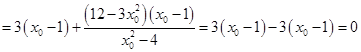 .
.所以
 .…………12分
.…………12分因为
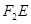 是以
是以 为直径的圆的半径,
为直径的圆的半径, 为圆心,
为圆心, ,故以
,故以 为直径的圆与直线
为直径的圆与直线 相切于右焦点.
相切于右焦点.
练习册系列答案
相关题目
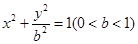 的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作
的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作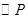 ,其中圆心P的坐标为
,其中圆心P的坐标为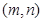 .(1) 若FC是
.(1) 若FC是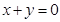 上,求椭圆的方程.
上,求椭圆的方程. 中,已知椭圆
中,已知椭圆 的离心率为
的离心率为 ,其焦点在圆
,其焦点在圆 上.
上. 、
、 、
、 是椭圆上的三点(异于椭圆顶点),且存在锐角
是椭圆上的三点(异于椭圆顶点),且存在锐角 ,使
,使 .
. 与
与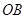 的斜率的乘积;
的斜率的乘积; 的值.
的值. 上一点
上一点 到右准线的距离为
到右准线的距离为 ,则该点到左焦点的距离为( )
,则该点到左焦点的距离为( ) 



 (a>b>0)的左右焦点分别为F1,F2,P是椭圆上一点。
(a>b>0)的左右焦点分别为F1,F2,P是椭圆上一点。 PF1F2为以F2P为底边的等腰三角形,当60°<
PF1F2为以F2P为底边的等腰三角形,当60°< PF1F2
PF1F2 的左、右焦点分别为
的左、右焦点分别为 ,若以
,若以 为圆心,
为圆心, 为半径作圆
为半径作圆 作此圆的切线,切点为
作此圆的切线,切点为 ,且
,且 的最小值不小于为
的最小值不小于为 .
. 的取值范围;
的取值范围; ,圆
,圆 轴的右交点为
轴的右交点为 ,过点
,过点 的直线
的直线 与椭圆相交于
与椭圆相交于 两点,若
两点,若 ,求直线
,求直线 的最大值.
的最大值.
 的左、右焦点分别为F1和F2 ,以F1、F2为直径的圆经过点M(0,b).(1)求椭圆的方程;(2)设直线l与椭圆相交于A,B两点,且
的左、右焦点分别为F1和F2 ,以F1、F2为直径的圆经过点M(0,b).(1)求椭圆的方程;(2)设直线l与椭圆相交于A,B两点,且 .求证:直线l在y轴上的截距为定值。
.求证:直线l在y轴上的截距为定值。 ,点M是线段AB上一点,且
,点M是线段AB上一点,且 点M随线段AB的滑动而运动.
点M随线段AB的滑动而运动. 的直线
的直线 交曲线E于C、D两点,交y轴于点P,若
交曲线E于C、D两点,交y轴于点P,若 的值
的值
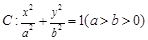 ,顺次连结椭圆
,顺次连结椭圆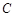 的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率
的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率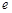 等于( ).
等于( ).


