题目内容
已知椭圆 的左、右焦点分别为F1和F2 ,以F1、F2为直径的圆经过点M(0,b).(1)求椭圆的方程;(2)设直线l与椭圆相交于A,B两点,且
的左、右焦点分别为F1和F2 ,以F1、F2为直径的圆经过点M(0,b).(1)求椭圆的方程;(2)设直线l与椭圆相交于A,B两点,且 .求证:直线l在y轴上的截距为定值。
.求证:直线l在y轴上的截距为定值。
 的左、右焦点分别为F1和F2 ,以F1、F2为直径的圆经过点M(0,b).(1)求椭圆的方程;(2)设直线l与椭圆相交于A,B两点,且
的左、右焦点分别为F1和F2 ,以F1、F2为直径的圆经过点M(0,b).(1)求椭圆的方程;(2)设直线l与椭圆相交于A,B两点,且 .求证:直线l在y轴上的截距为定值。
.求证:直线l在y轴上的截距为定值。(1)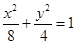 (2)
(2)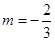 .直线l在y轴上的截距为定值
.直线l在y轴上的截距为定值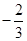
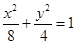 (2)
(2)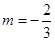 .直线l在y轴上的截距为定值
.直线l在y轴上的截距为定值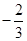
本试题主要是考查了椭圆的方程的求解,直线与椭圆的位置关系的综合运问题,以及韦达定理的综合运用。
(1)利用椭圆的性质可知参数a,b,c的值,求解得到椭圆的方程。
(2)因为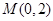 ,所以直线
,所以直线 与x轴不垂直.设直线
与x轴不垂直.设直线 的方程为
的方程为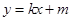 ,然后直线与椭圆联立方程组,借助于韦达定理来解决
,然后直线与椭圆联立方程组,借助于韦达定理来解决
(1)由题设知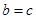 ,又
,又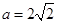 ,所以
,所以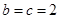 ,故椭圆方程为
,故椭圆方程为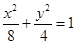 ;……2分
;……2分
(2)因为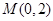 ,所以直线
,所以直线 与x轴不垂直.设直线
与x轴不垂直.设直线 的方程为
的方程为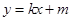 ,
,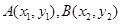 由
由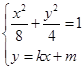 得
得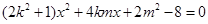 ,所以
,所以
 …………………6分
…………………6分
又 ,所以
,所以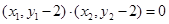 ,即
,即 ,
,
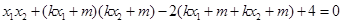 ,
,
整理得 ,
,
即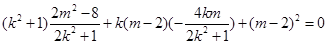 ,…………10分
,…………10分
因为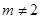 ,所以
,所以 ,
,
展开整理得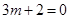 ,即
,即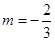 .直线l在y轴上的截距为定值
.直线l在y轴上的截距为定值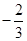
(1)利用椭圆的性质可知参数a,b,c的值,求解得到椭圆的方程。
(2)因为
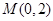 ,所以直线
,所以直线 与x轴不垂直.设直线
与x轴不垂直.设直线 的方程为
的方程为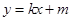 ,然后直线与椭圆联立方程组,借助于韦达定理来解决
,然后直线与椭圆联立方程组,借助于韦达定理来解决(1)由题设知
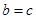 ,又
,又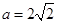 ,所以
,所以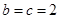 ,故椭圆方程为
,故椭圆方程为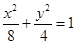 ;……2分
;……2分(2)因为
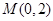 ,所以直线
,所以直线 与x轴不垂直.设直线
与x轴不垂直.设直线 的方程为
的方程为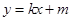 ,
,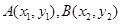 由
由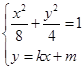 得
得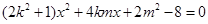 ,所以
,所以 …………………6分
…………………6分又
 ,所以
,所以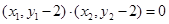 ,即
,即 ,
,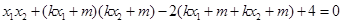 ,
,整理得
 ,
,即
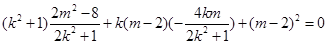 ,…………10分
,…………10分因为
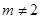 ,所以
,所以 ,
,展开整理得
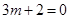 ,即
,即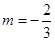 .直线l在y轴上的截距为定值
.直线l在y轴上的截距为定值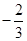

练习册系列答案
相关题目
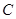 :
: 的左、右顶点分别为
的左、右顶点分别为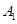 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 ,离心率是
,离心率是 .
. 是椭圆
是椭圆 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 (
( 在横坐标为
在横坐标为 的点处的切线为L,则点(3,2)到L的距离是
的点处的切线为L,则点(3,2)到L的距离是



 的直线l过椭圆
的直线l过椭圆 的焦点以及点(0,
的焦点以及点(0, ),直线l与椭圆C交于 A 、B 两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B 两点,且A、B两点与另一焦点围成的三角形周长为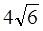 。
。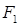 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点, (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程 (a>b>0)的离心率为
(a>b>0)的离心率为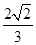 ,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.
 的一个顶点为A(2,0),离心率为
的一个顶点为A(2,0),离心率为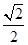 ,直线
,直线 与椭圆C交于不同的两点M,N。
与椭圆C交于不同的两点M,N。 的面积为
的面积为 时,求k的值。
时,求k的值。 :
: (
( ),直线
),直线 为圆
为圆 :
: 的一条切线并且过椭圆的右焦点,记椭圆的离心率为
的一条切线并且过椭圆的右焦点,记椭圆的离心率为 .
. ,求
,求 的离心率是 ( )
的离心率是 ( )



 上一点,F1、F2是椭圆的两个焦点,
上一点,F1、F2是椭圆的两个焦点, ,则△F1PF2的面积是 .
,则△F1PF2的面积是 .