题目内容
(本题12分)在平面直角坐标系 中,已知椭圆
中,已知椭圆 的离心率为
的离心率为 ,其焦点在圆
,其焦点在圆 上.
上.
⑴求椭圆的方程;
⑵设 、
、 、
、 是椭圆上的三点(异于椭圆顶点),且存在锐角
是椭圆上的三点(异于椭圆顶点),且存在锐角 ,使
,使 .
.
①试求直线 与
与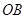 的斜率的乘积;
的斜率的乘积;
②试求 的值.
的值.
 中,已知椭圆
中,已知椭圆 的离心率为
的离心率为 ,其焦点在圆
,其焦点在圆 上.
上.⑴求椭圆的方程;
⑵设
 、
、 、
、 是椭圆上的三点(异于椭圆顶点),且存在锐角
是椭圆上的三点(异于椭圆顶点),且存在锐角 ,使
,使 .
.①试求直线
 与
与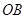 的斜率的乘积;
的斜率的乘积;②试求
 的值.
的值.(1)  .(2) (i)
.(2) (i)  ,
,
(ii) =
=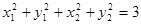 .
.
 .(2) (i)
.(2) (i)  ,
,(ii)
 =
=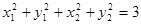 .
.(1)易知焦点坐标为(-1,0),(1,0),再根据离心率求出a,进而求出b的值.从而确定椭圆的方程.
(2)设 ,设
,设 ,因
,因 ,
,
故 ,再根据M在椭圆上,可得
,再根据M在椭圆上,可得 ,
,
然后再利用点A、B在椭圆上这个条件,得到两个方程,以此对上面的方程化简,可求出直线 与
与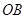 的斜率的乘积.
的斜率的乘积.
(ii) 因为 =
=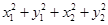 ,然后可以根据(i)的结论,得到
,然后可以根据(i)的结论,得到 ,
,
从而 ,又因
,又因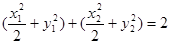 ,所以
,所以 .问题到此得以解决.
.问题到此得以解决.
(1)依题意得 , 于是
, 于是 .
.
所以所求椭圆的方程为 .
.
(2) (i)设 ,则
,则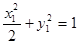 ①
①
 ②.
②.
又设 ,因
,因 ,
,
故
因 在椭圆上,
在椭圆上,
故
整理得:
将①②代入上式,并由 得
得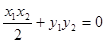
所以
(ii) ,
,
故
又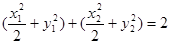
故
所以, =
=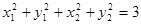 .
.
(2)设
 ,设
,设 ,因
,因 ,
,故
 ,再根据M在椭圆上,可得
,再根据M在椭圆上,可得 ,
,然后再利用点A、B在椭圆上这个条件,得到两个方程,以此对上面的方程化简,可求出直线
 与
与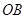 的斜率的乘积.
的斜率的乘积.(ii) 因为
 =
=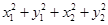 ,然后可以根据(i)的结论,得到
,然后可以根据(i)的结论,得到 ,
,从而
 ,又因
,又因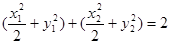 ,所以
,所以 .问题到此得以解决.
.问题到此得以解决.(1)依题意得
 , 于是
, 于是 .
. 所以所求椭圆的方程为
 .
.(2) (i)设
 ,则
,则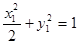 ①
① ②.
②.又设
 ,因
,因 ,
,故

因
 在椭圆上,
在椭圆上,故

整理得:

将①②代入上式,并由
 得
得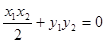
所以

(ii)
 ,
,故

又
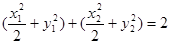
故

所以,
 =
=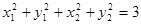 .
.
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
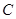 :
: 的左、右顶点分别为
的左、右顶点分别为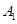 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 ,离心率是
,离心率是 .
. 是椭圆
是椭圆 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 (
( 的焦点,离心率是
的焦点,离心率是
 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由. 在横坐标为
在横坐标为 的点处的切线为L,则点(3,2)到L的距离是
的点处的切线为L,则点(3,2)到L的距离是



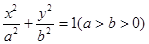 上有一动点P,P到椭圆C的两焦点 F1,F2的距离之和等于2
上有一动点P,P到椭圆C的两焦点 F1,F2的距离之和等于2 ,△PF1F2的面积最大值为1
,△PF1F2的面积最大值为1 (O为坐标原点)且
(O为坐标原点)且 | ,求实数t的取值范围.
| ,求实数t的取值范围.  ,
,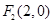 ,曲线
,曲线 上的动点
上的动点 满足
满足 ,直线
,直线 与曲线
与曲线 .
. ,若
,若
 ,求直线
,求直线 的方程.
的方程.
 的一个顶点为A(2,0),离心率为
的一个顶点为A(2,0),离心率为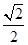 ,直线
,直线 与椭圆C交于不同的两点M,N。
与椭圆C交于不同的两点M,N。 的面积为
的面积为 时,求k的值。
时,求k的值。 的焦点为
的焦点为 和
和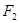 ,点
,点 在椭圆上,如果线段
在椭圆上,如果线段 的中点在
的中点在 轴上,那么
轴上,那么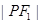 是
是 的( )
的( ) 倍
倍 倍
倍 倍
倍 倍
倍 的离心率是 ( )
的离心率是 ( )


