题目内容
如图,线段AB的两个端点A、B分别在x轴,y轴上滑动, ,点M是线段AB上一点,且
,点M是线段AB上一点,且 点M随线段AB的滑动而运动.
点M随线段AB的滑动而运动.
(I)求动点M的轨迹E的方程
(II)过定点N 的直线
的直线 交曲线E于C、D两点,交y轴于点P,若
交曲线E于C、D两点,交y轴于点P,若 的值
的值
 ,点M是线段AB上一点,且
,点M是线段AB上一点,且 点M随线段AB的滑动而运动.
点M随线段AB的滑动而运动.(I)求动点M的轨迹E的方程
(II)过定点N
 的直线
的直线 交曲线E于C、D两点,交y轴于点P,若
交曲线E于C、D两点,交y轴于点P,若 的值
的值
(I) ;(II)-8.
;(II)-8.
 ;(II)-8.
;(II)-8.(1)本小题属于相关点法求轨迹方程,设 ,可以用
,可以用 表示
表示 ,
,
再代入 ,可得动点M的轨迹方程.
,可得动点M的轨迹方程.
(II)由条件不难判断直线L的斜率存在,然后设其方程为 与动点M的轨迹方程联立消y后得到关于x的一元二次方程,然后借助韦达定理,判断式来解决是解决此类问题的基本思路.本小题设
与动点M的轨迹方程联立消y后得到关于x的一元二次方程,然后借助韦达定理,判断式来解决是解决此类问题的基本思路.本小题设 ,则
,则 然后将韦达定理代入式子证明即可.
然后将韦达定理代入式子证明即可.
解:(I)设 ,得
,得

∴动点M的轨迹E的方程为
(II)显然,直线L的斜率存在,设其方程为 即
即
 ,令
,令 联立
联立 得
得

即



 ,可以用
,可以用 表示
表示 ,
,再代入
 ,可得动点M的轨迹方程.
,可得动点M的轨迹方程.(II)由条件不难判断直线L的斜率存在,然后设其方程为
 与动点M的轨迹方程联立消y后得到关于x的一元二次方程,然后借助韦达定理,判断式来解决是解决此类问题的基本思路.本小题设
与动点M的轨迹方程联立消y后得到关于x的一元二次方程,然后借助韦达定理,判断式来解决是解决此类问题的基本思路.本小题设 ,则
,则 然后将韦达定理代入式子证明即可.
然后将韦达定理代入式子证明即可.解:(I)设
 ,得
,得
∴动点M的轨迹E的方程为

(II)显然,直线L的斜率存在,设其方程为
 即
即 ,令
,令 联立
联立 得
得
即





练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
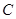 :
: 的左、右顶点分别为
的左、右顶点分别为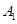 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 ,离心率是
,离心率是 .
. 是椭圆
是椭圆 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 (
( ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
.
 的一个顶点为A(2,0),离心率为
的一个顶点为A(2,0),离心率为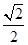 ,直线
,直线 与椭圆C交于不同的两点M,N。
与椭圆C交于不同的两点M,N。 的面积为
的面积为 时,求k的值。
时,求k的值。 ,直线
,直线 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重合,
轴重合,  ,两点,当
,两点,当 ,若点
,若点 且
且
 的方程;
的方程; 交于
交于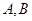 两点,若
两点,若 ,求
,求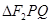 的面积
的面积 的取值范围(
的取值范围( 为椭圆的右焦点)。
为椭圆的右焦点)。 为椭圆
为椭圆 的两个焦点,P为椭圆上一点且
的两个焦点,P为椭圆上一点且 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )



 :
: (
( ),直线
),直线 为圆
为圆 :
: 的一条切线并且过椭圆的右焦点,记椭圆的离心率为
的一条切线并且过椭圆的右焦点,记椭圆的离心率为 .
. ,求
,求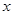 轴上,离心率为
轴上,离心率为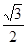 ,它与直线
,它与直线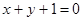 相交于P、Q两点,若
相交于P、Q两点,若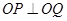 ,求椭圆方程。
,求椭圆方程。 上一点,F1、F2是椭圆的两个焦点,
上一点,F1、F2是椭圆的两个焦点, ,则△F1PF2的面积是 .
,则△F1PF2的面积是 .