题目内容
(本小题满分14分)(注意:在试题卷上作答无效)
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,若以
,若以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,过椭圆上一点
,过椭圆上一点 作此圆的切线,切点为
作此圆的切线,切点为 ,且
,且 的最小值不小于为
的最小值不小于为 .
.
(1)求椭圆的离心率 的取值范围;
的取值范围;
(2)设椭圆的短半轴长为 ,圆
,圆 与
与 轴的右交点为
轴的右交点为 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 与椭圆相交于
与椭圆相交于 两点,若
两点,若 ,求直线
,求直线 被圆
被圆 截得的弦长
截得的弦长 的最大值.
的最大值.
已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,若以
,若以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,过椭圆上一点
,过椭圆上一点 作此圆的切线,切点为
作此圆的切线,切点为 ,且
,且 的最小值不小于为
的最小值不小于为 .
.(1)求椭圆的离心率
 的取值范围;
的取值范围;(2)设椭圆的短半轴长为
 ,圆
,圆 与
与 轴的右交点为
轴的右交点为 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 与椭圆相交于
与椭圆相交于 两点,若
两点,若 ,求直线
,求直线 被圆
被圆 截得的弦长
截得的弦长 的最大值.
的最大值.
(1) ;(2)
;(2)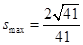 .
.
 ;(2)
;(2)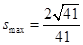 .
.(1)根据圆的切线长公式可得 ,显然当
,显然当 取得最小值时
取得最小值时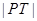 取得最小值,而
取得最小值,而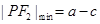 ,再根据
,再根据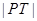 的最小值为
的最小值为 ,可建立关于a,c的不等式,从而求出e的取值范围.
,可建立关于a,c的不等式,从而求出e的取值范围.
(2)设直线l的方程为 ,然后与椭圆方程联立消y得关于x的一元二次方程,因为
,然后与椭圆方程联立消y得关于x的一元二次方程,因为 ,所以
,所以 再结合直线方程和韦达定理,建立关于k与a的等式关系.从而在直线方程中用a表示k,再把
再结合直线方程和韦达定理,建立关于k与a的等式关系.从而在直线方程中用a表示k,再把 最终化成关于c的函数表达式,再利用率心率e的范围,确定出c的范围,求函数最值即可.
最终化成关于c的函数表达式,再利用率心率e的范围,确定出c的范围,求函数最值即可.
(1)依题意设切线长
∴当且仅当 取得最小值时
取得最小值时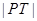 取得最小值,
取得最小值,
而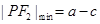 ,......2分
,......2分
 ,
,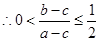 ,
,
从而解得 ,故离心率
,故离心率 的取值范围是
的取值范围是 ;......6分
;......6分
(2)依题意 点的坐标为
点的坐标为 ,则直线的方程为
,则直线的方程为 , 联立方程组
, 联立方程组 
得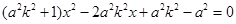 ,设
,设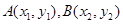 ,则有
,则有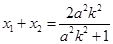 ,
, ,代入直线方程得
,代入直线方程得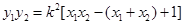
 ,
,
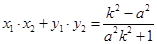 ,又
,又 ,
,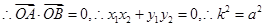 ,
,
...... 10分
 ,直线的方程为
,直线的方程为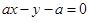 ,圆心
,圆心
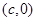 到直线
到直线 的距离
的距离 ,由图象可知
,由图象可知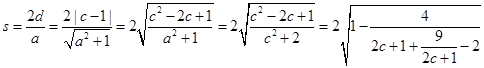 ,
,
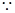
 ,
, ,
,
 ,所以
,所以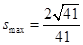 .14分
.14分
 ,显然当
,显然当 取得最小值时
取得最小值时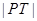 取得最小值,而
取得最小值,而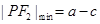 ,再根据
,再根据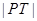 的最小值为
的最小值为 ,可建立关于a,c的不等式,从而求出e的取值范围.
,可建立关于a,c的不等式,从而求出e的取值范围.(2)设直线l的方程为
 ,然后与椭圆方程联立消y得关于x的一元二次方程,因为
,然后与椭圆方程联立消y得关于x的一元二次方程,因为 ,所以
,所以 再结合直线方程和韦达定理,建立关于k与a的等式关系.从而在直线方程中用a表示k,再把
再结合直线方程和韦达定理,建立关于k与a的等式关系.从而在直线方程中用a表示k,再把 最终化成关于c的函数表达式,再利用率心率e的范围,确定出c的范围,求函数最值即可.
最终化成关于c的函数表达式,再利用率心率e的范围,确定出c的范围,求函数最值即可.(1)依题意设切线长

∴当且仅当
 取得最小值时
取得最小值时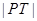 取得最小值,
取得最小值,而
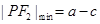 ,......2分
,......2分 ,
,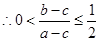 ,
,从而解得
 ,故离心率
,故离心率 的取值范围是
的取值范围是 ;......6分
;......6分(2)依题意
 点的坐标为
点的坐标为 ,则直线的方程为
,则直线的方程为 , 联立方程组
, 联立方程组 
得
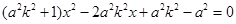 ,设
,设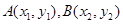 ,则有
,则有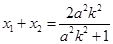 ,
, ,代入直线方程得
,代入直线方程得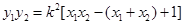
 ,
,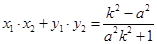 ,又
,又 ,
,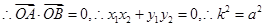 ,
,...... 10分
 ,直线的方程为
,直线的方程为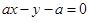 ,圆心
,圆心
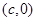 到直线
到直线 的距离
的距离 ,由图象可知
,由图象可知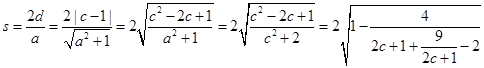 ,
,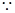
 ,
, ,
,
 ,所以
,所以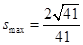 .14分
.14分
练习册系列答案
相关题目
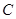 :
: 的左、右顶点分别为
的左、右顶点分别为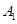 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 ,离心率是
,离心率是 .
. 是椭圆
是椭圆 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 (
( ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. 的离心率为
的离心率为 ,直线
,直线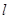 :
: 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. ,右焦点
,右焦点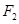 ,直线
,直线 过点
过点 垂
垂 ,线段
,线段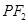 垂直平分线交
垂直平分线交 ,求点
,求点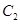 的方程;
的方程;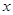 轴上时,在曲线
轴上时,在曲线 ,
,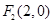 ,曲线
,曲线 上的动点
上的动点 满足
满足 ,直线
,直线 与曲线
与曲线 .
. ,若
,若
 ,求直线
,求直线 的方程.
的方程. 中,满足
中,满足 ,
, .若一个椭圆恰好以
.若一个椭圆恰好以 为一个焦点,另一个焦点在线段
为一个焦点,另一个焦点在线段 上,且
上,且 ,
, 均在此椭圆上,则该椭圆的离心率为 .
均在此椭圆上,则该椭圆的离心率为 . 的直线l过椭圆
的直线l过椭圆 的焦点以及点(0,
的焦点以及点(0, ),直线l与椭圆C交于 A 、B 两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B 两点,且A、B两点与另一焦点围成的三角形周长为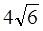 。
。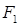 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点, (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程 的离心率是 ( )
的离心率是 ( )



 上一点,F1、F2是椭圆的两个焦点,
上一点,F1、F2是椭圆的两个焦点, ,则△F1PF2的面积是 .
,则△F1PF2的面积是 .