题目内容
9．${（1-\sqrt{x}）^5}$的展开式中x2的系数是（ ）| A． | -5 | B． | 5 | C． | -10 | D． | 10 |
分析 在二项展开式的通项公式中，令x的幂指数等于2，求出r的值，即可求得展开式中x2的系数．
解答 解：${（1-\sqrt{x}）^5}$的展开式的通项公式为 Tr+1=${C}_{5}^{r}$•（-$\sqrt{x}$）r，
令r=4，可得展开式中x2的系数为5，
故选：B．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，属于中档题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
19．等比数列{an}中，任意的n∈N*，an+1+an=3n+1，则公比q等于（ ）
| A． | 2 | B． | 3 | C． | $\sqrt{3}$ | D． | -$\sqrt{3}$ |
17．已知椭圆C1与抛物线C2的焦点均在x轴上，C1的中心和C2的顶点为原点O，从椭圆C1上取两个点，从椭圆C2上取一个点，将其坐标记录于表中：
（1）试判断两个点在C1上，并求出C1，C2的标准方程；
（2）已知直线l：x=my+1与椭圆C2相交于不同两点M，N，且满足$\overrightarrow{OM}⊥\overrightarrow{ON}$，求参数m的值．
| x | $\sqrt{2}$ | 2 | 4 |
| y | $\frac{\sqrt{2}}{2}$ | 0 | 4 |
（2）已知直线l：x=my+1与椭圆C2相交于不同两点M，N，且满足$\overrightarrow{OM}⊥\overrightarrow{ON}$，求参数m的值．
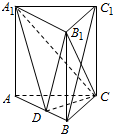已知三棱柱ABC-A1B1C1中，侧棱垂直于底面，AC=BC，点D是AB的中点．求证：
1．若（x-2）n展开式中共有12项，则n=（ ）
| A． | 10 | B． | 11 | C． | 12 | D． | 13 |