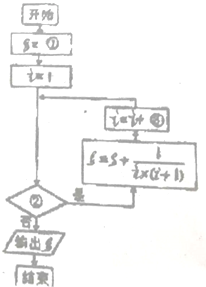
题目内容
1.若(x-2)n展开式中共有12项,则n=( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
分析 直接利用二项式定理的性质写出结果即可.
解答 解:若(x-2)n展开式中共有12项,则n=11.
故选:B.
点评 本题考查二项式定理的简单性质的应用,基本知识的考查.

练习册系列答案
相关题目
9.${(1-\sqrt{x})^5}$的展开式中x2的系数是( )
| A. | -5 | B. | 5 | C. | -10 | D. | 10 |
11.两直线ax+by+4=0和(1-a)x-y-b=O都平行于x+2y+3=0,则( )
| A. | $\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=3}\end{array}\right.$ |
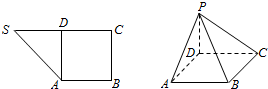 如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB. 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=$\frac{π}{2}$,AD=2$\sqrt{2}$,AB=3DC=3.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=$\frac{π}{2}$,AD=2$\sqrt{2}$,AB=3DC=3.