题目内容
9．某几何体的三视图如图所示，图中3个三角表均为直角三角形，则该几何体的体积的最大值$\frac{1}{2}$．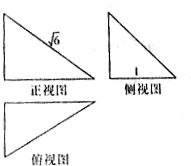
分析 几何体是一个三棱锥，三棱锥的底面是一条直角边为1，另一条直角边不妨设为b，三棱锥的一条侧棱与底面垂直，不妨设为a，进而可得：a2+b2=6，进而表示出体积，根据不等式基本定理，得到最值．
解答 解：由三视图知，几何体是一个三棱锥，
三棱锥的底面是一条直角边为1，另一条直角边不妨设为b，
三棱锥的一条侧棱与底面垂直，不妨设为a，
由勾股定理可知a2+b2=6≥2ab，
即ab≤3，
∴几何体的体积是V=$\frac{1}{3}$×$\frac{1}{2}$×1×a×b=$\frac{ab}{6}$≤$\frac{1}{2}$
∴V的最大值为$\frac{1}{2}$，当且仅当a=b时取得最大值，
故答案为：$\frac{1}{2}$
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
19．设函数f（x）=（x-a）2+（lnx2-2a）2，其中x＞0，a∈R，存在x0使得f（x0）$≤\frac{4}{5}$成立，则实数a值是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{1}{2}$ | D． | 1 |
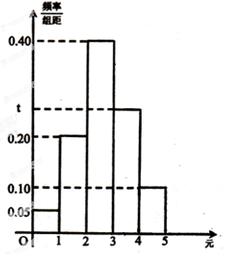春节期间，某微信群主发60个随机红包（即每个人抢到的红包中的钱数是随机的，且每人只能抢一个），红包被一抢而空，后据统计，60个红包中钱数（单位：元）分配如下频率分布直方图所示（其分组区间为[0，1），[1，2），[2，3），[3，4），[4，5））．
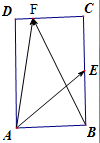如图，在矩形ABCD中，AB=$\sqrt{2}$，BC=2，点E为BC的中点，点F在边CD上，若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$，求$\overrightarrow{AE}$•$\overrightarrow{AF}$．
如图，四棱锥P-ABCD，底面ABCD为正方形，PA=PD，PA⊥平面PDC，E为棱PD的中点