题目内容
【题目】已知函数f(x)=alnx+ ![]() ,曲线f(x)在点(1,f(1))处的切线平行于x轴.
,曲线f(x)在点(1,f(1))处的切线平行于x轴.
(1)求f(x)的最小值;
(2)比较f(x)与 ![]() 的大小;
的大小;
(3)证明:x>0时,xexlnx+ex>x3 .
【答案】
(1)解:f'(x)= ![]() ,根据题意知f'(1)=0,即a=1,∴
,根据题意知f'(1)=0,即a=1,∴ ![]() ,
,
∴f'(x)= ![]() ,∴当0<x<1时,f'(x)<0,f(x)单调递减;
,∴当0<x<1时,f'(x)<0,f(x)单调递减;
当x>1时,f'(x)>0,f(x)单调递增;
∴f(x)min=f(1)=1
(2)解:令 ![]() =
= ![]() =
= ![]() ,
,
![]() ,
,
∴g(x)在(0,+∞)上单调递减
又∵g(1)=0∴当0<x<1时,g(x)>g(1)=0, ![]() ;
;
当x>1时,g(x)<g(1)=0, ![]() ;
;
当x=1时,g(x)=0, ![]()
(3)证明:要证xexlnx+ex>x3,即证: ![]()
令 ![]() ,即证∴f(x)>h(x),
,即证∴f(x)>h(x), ![]() =
= ![]() ,
,
∴当0<x<2时,h'(x)>0,h(x)单调递增;
当x>2时,h'(x)<0,h(x)单调递减;∴h(x)max=h(2)= ![]() ,
,
又由(1)知f(x)min=1,∴f(x)≥1,∴f(x)>h(x),得证
【解析】(1)求出函数的导数,利用曲线f(x)在点(1,f(1))处的切线平行于x轴,求出a,然后判断函数的单调性,求解函数的最小值即可.(2)令 ![]() ,化简通过函数的导数,判断导函数的符号,然后通过x 的范围,判断两个数的大小.(3)要证xexlnx+ex>x3 , 即证:
,化简通过函数的导数,判断导函数的符号,然后通过x 的范围,判断两个数的大小.(3)要证xexlnx+ex>x3 , 即证: ![]() ,令
,令 ![]() ,利用函数的导数,判断函数的单调性求出函数的最小值,即可证明结果.
,利用函数的导数,判断函数的单调性求出函数的最小值,即可证明结果.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.

【题目】如图,A,B,C是椭圆M:![]() 上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
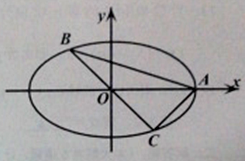
(1)求椭圆的离心率;
(2)若y轴被△ABC的外接圆所截得弦长为9,求椭圆方程。
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.

