题目内容
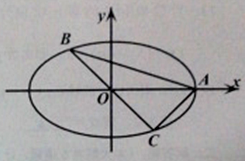
【题目】如图,A,B,C是椭圆M:![]() 上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
(1)求椭圆的离心率;
(2)若y轴被△ABC的外接圆所截得弦长为9,求椭圆方程。
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)有条件列出C点坐标是解题关键:因为![]() 过椭圆
过椭圆![]() 的中心,所以
的中心,所以![]() ,又
,又![]() ,所以
,所以![]() 是以角
是以角![]() 为直角的等腰直角三角形,则
为直角的等腰直角三角形,则![]() 所以
所以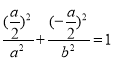 ,则
,则![]() ,
,![]() (2)本题关键为表示出△ABC的外接圆方程:
(2)本题关键为表示出△ABC的外接圆方程:![]() 的外接圆直径为AB,所以易得
的外接圆直径为AB,所以易得![]() 的外接圆为:
的外接圆为:![]() ,由垂径定理得
,由垂径定理得![]() 即
即![]() ,所以椭圆方程为
,所以椭圆方程为![]() .
.
试题解析:(1)因为![]() 过椭圆
过椭圆![]() 的中心,所以
的中心,所以![]() ,
,
又![]() ,所以
,所以![]() 是以角
是以角![]() 为直角的等腰直角三角形, 3分
为直角的等腰直角三角形, 3分
则![]() ,所以
,所以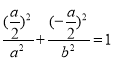 ,则
,则![]() ,
,
所以![]() ; 7分
; 7分
(2)![]() 的外接圆圆心为
的外接圆圆心为![]() 中点
中点![]() ,半径为
,半径为![]() ,
,
则![]() 的外接圆为:
的外接圆为:![]() 10分
10分
令![]() ,
,![]() 或
或![]() ,所以
,所以![]() ,得
,得![]() ,
,
(也可以由垂径定理得![]() 得
得![]() )
)
所以所求的椭圆方程为![]() . 15分
. 15分

练习册系列答案
相关题目
【题目】为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
据上表得回归直线方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,据此估计,该社区一户收入为15万元家庭年支出为( )
,据此估计,该社区一户收入为15万元家庭年支出为( )
A.11.4万元
B.11.8万元
C.12.0万元
D.12.2万元