题目内容
【题目】如图，已知椭圆C：
1（a＞b＞0）的右焦点为F，A（2，0）是椭圆的右顶点，过F且垂直于x轴的直线交椭圆于P，Q两点，且|PQ|＝3．
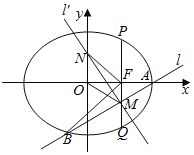
（1）求椭圆的方程；
（2）过点A的直线l与椭圆交于另一点B，垂直于l的直线l′与直线l交于点M，与y轴交于点N，若FB⊥FN且|MO|＝|MA|，求直线l的方程．
【答案】（1）
（2）直线l方程为：x＝±
y+2
【解析】
（1）由
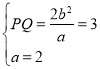得：
，
，即可求出椭圆方程，
（2）由于直线
过点
，可设 方程为：
，求出点
，
的坐标，根据向量的数量积和点在椭圆上，即可求出
的值，即可求出直线的方程
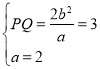解：（1）由得：，，
所以椭圆方程为
，
（2）由于直线过点，可设 方程为：，由题意可知
，与直线
联立，得
，
直线
与直线垂直，可得直线方程为：
令
．得
，设
，
，
，
所以
，即
①，
由
点在椭圆上，代入椭圆方程得：
②，联立①②，得
，
所以直线方程为：
，
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物），为了探究车流量与PM2.5的浓度是否相关，现采集到某城市周一至周五某一时间段车流量与PM2.5浓度的数据如下表：
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x（万辆） | 100 | 102 | 108 | 114 | 116 |
PM2.5的浓度y（微克/立方米） | 78 | 80 | 84 | 88 | 90 |
（1）根据上表数据，用最小二乘法，求出y关于x的线性回归方程
x
；
（2）若周六同一时间段车流量200万辆，试根据（1）求出的线性回归方程，预测此时PM2.5的浓度为多少？
（参考公式：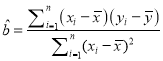
，
；参考数据：
xi＝540，yi＝420）
