题目内容
【题目】某机构对A市居民手机内安装的“APP”(英文Application的缩写,一般指手机软件)的个数和用途进行调研,在使用智能手机的居民中随机抽取了100人,获得了他们手机内安装APP的个数,整理得到如图所示频率分布直方图:
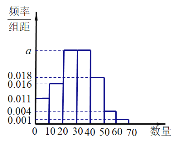
(Ⅰ)从A市随机抽取一名使用智能手机的居民,试估计该居民手机内安装APP的个数不低于30的概率;
(Ⅱ)从A市随机抽取3名使用智能手机的居民进一步做调研,用X表示这3人中手机内安装APP的个数在[20,40)的人数.
①求随机变量X的分布列及数学期望;
②用Y1表示这3人中安装APP个数低于20的人数,用Y2表示这3人中手机内安装APP的个数不低于40的人数.试比较EY1和EY2的大小.(只需写出结论)
【答案】(Ⅰ)0.48;(Ⅱ)①详见解析;②![]() .
.
【解析】
(Ⅰ)先求出a的值,再求该居民手机内安装“APP”的数量不低于30的概率估计为
![]() ;(Ⅱ)①由题得
;(Ⅱ)①由题得![]() 所有的可能取值为0,1,2,3,则X∽B(3,
所有的可能取值为0,1,2,3,则X∽B(3,![]() ),再求随机变量X的分布列及数学期望;②根据频率分布直方图计算可得
),再求随机变量X的分布列及数学期望;②根据频率分布直方图计算可得![]() .
.
解:(Ⅰ)由![]() 得
得![]() .
.
从![]() 市随机抽取一名使用智能手机的居民,该居民手机内安装“APP”的数量不低于30的概率估计为
市随机抽取一名使用智能手机的居民,该居民手机内安装“APP”的数量不低于30的概率估计为![]() .
.
(Ⅱ)①从![]() 市随机抽取一名使用智能手机的居民,该居民手机内安装“APP”的数量在
市随机抽取一名使用智能手机的居民,该居民手机内安装“APP”的数量在
![]() 的概率估计为
的概率估计为![]() .
.
![]() 所有的可能取值为0,1,2,3,则X∽B(3,
所有的可能取值为0,1,2,3,则X∽B(3,![]() ).
).
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() 的数学期望为
的数学期望为
![]() .(或者
.(或者![]() .)
.)
②![]() .
.

【题目】“有黑扫黑、无黑除恶、无恶治乱”,维护社会稳定和和平发展.扫黑除恶期间,大量违法分子主动投案,某市公安机关对某月连续7天主动投案的人员进行了统计,![]() 表示第
表示第![]() 天主动投案的人数,得到统计表格如下:
天主动投案的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判定变量![]() 与
与![]() 之间是正相关还是负相关.(写出正确答案,不用说明理由)
之间是正相关还是负相关.(写出正确答案,不用说明理由)
(3)预测第八天的主动投案的人数(按四舍五入取到整数).
参考公式: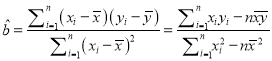 ,
, ![]() .
.
【题目】为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后,发布了《个人所得税专项附加扣除暂行办法》,明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用,并公布了相应的定额扣除标准,决定自2019年1月1日起施行,某机关为了调查内部职员对新个税方案的满意程度与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁及以下 | 40岁以上 | 合计 | |
基本满意 | 15 | 10 | 25 |
很满意 | 25 | 30 | 55 |
合计 | 40 | 40 | 80 |
(1)根据列联表,能否有85%的把握认为满意程度与年龄有关?
(2)若已经在满意程度为“基本满意”的职员中用分层抽样的方式选取了5名职员,现从这5名职员中随机选取3名进行面谈求面谈的职员中恰有2名年龄在40岁及以下的概率.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |