题目内容
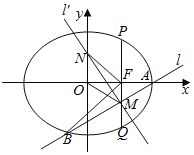
【题目】在直角坐标系![]() 中,过点
中,过点![]() 作直线
作直线![]() 交
交![]() 轴于A点、交
轴于A点、交![]() 轴于B点,且P位于AB两点之间.
轴于B点,且P位于AB两点之间.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)求当![]() 取得最小值时直线
取得最小值时直线![]() 的方程;
的方程;
(3)当![]() 面积最小值时的直线方程.
面积最小值时的直线方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
设直线![]() 可求出
可求出![]() ,
,![]() .结合
.结合![]() 位于
位于![]() 之间,建立关于
之间,建立关于![]() 的不等式,可得
的不等式,可得![]() .
.
(1)由![]() 的坐标,得出向量
的坐标,得出向量![]() 和
和![]() 坐标,从而将
坐标,从而将![]() 化为关于
化为关于![]() 的方程,解出
的方程,解出![]() 值,即得直线
值,即得直线![]() 的方程;
的方程;
(2)由向量数量积的坐标运算公式,得出![]() 关于
关于![]() 的表达式,再用基本不等式得到
的表达式,再用基本不等式得到![]() 取得最小值时
取得最小值时![]() 的斜率
的斜率![]() ,从而得到直线
,从而得到直线![]() 的方程.
的方程.
(3)求出![]() ,再利用基本不等式求最小值,从而得到等号成立的条件,即
,再利用基本不等式求最小值,从而得到等号成立的条件,即![]() ,由此能求出当
,由此能求出当![]() 面积最小值时的直线方程.
面积最小值时的直线方程.
由题意知,直线![]() 的斜率
的斜率![]() 存在且
存在且![]() ,
,
设![]() ,得令
,得令![]() ,得
,得![]() ,所以
,所以![]() ,
,
再令![]() ,得
,得![]() ,所以
,所以![]() ,
,
∵点![]() 位于
位于![]() 两点之间,∴
两点之间,∴![]() 且
且![]() ,解得
,解得![]() .
.
∴![]() ,
,![]() ,
,
(1)∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∴直线![]() 的方程为
的方程为![]() ,整理得
,整理得![]() .
.
(2)∵![]() ,∴
,∴![]() ,
,
当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
∴当![]() 取得最小值时直线
取得最小值时直线![]() 的方程为
的方程为![]() ,
,
化为一般式:![]() .
.
(3)∵![]() ,
,![]() ,
,![]() ,
,
∴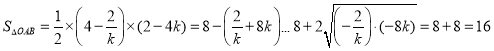 ,
,
当![]() 时,即
时,即![]() 时,取等号,
时,取等号,
∴当![]() 面积最小值时的直线方程为
面积最小值时的直线方程为![]() ,即
,即![]() .
.

练习册系列答案
相关题目