Question

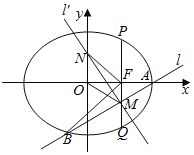
【题目】平面直角坐标系xOy中，抛物线的焦点为F，过F的动直线l交于M、N两点.

（1）若l垂直于x轴，且线段MN的长为1，求的方程；

（2）若，求线段MN的中点P的轨迹方程；

（3）求的取值范围.

Answer 1

【答案】（1）

（2）

（3）

【解析】

（1）由题意，（，±）在抛物线上，代入可求出p，问题得一解决，

（2）利用点差法和中点坐标公式和点斜式方程即可求出，

（3）抛物线Γ：y2＝2px（p＞0），设l：xmy，M（x1，y1），y1＞0，N（x2，y2），y2＜0根据根系数的关系和两角和的正切公式，化简整理即可求出．

解：（1）由题意，（，±）在抛物线上，代入可求出p，

∴Γ的方程为y2＝x，

（2）抛物线Γ：y2＝4x，设M（x1，y1），N（x2，y2），P（x0，y0）

∴，

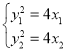∴（y1+y2）（y1﹣y2）＝4（x1+x2），

∴k，

于是l为y﹣y0（x﹣x0），

又l过点F（1，0），

∴﹣y0（1﹣x0），

即y02＝2（x0﹣1），

故线段MN的中点P的轨迹方程为y2＝2（x﹣1）

（3）抛物线Γ：y2＝2px（p＞0），设l：xmy，M（x1，y1），y1＞0，N（x2，y2），y2＜0，

则y2﹣2my﹣p2＝0，

∴y1+y2＝2mp，y1y2＝﹣p2，

则tan∠MON＝tan（∠MOF+∠NOF），

，

，

，

，

，

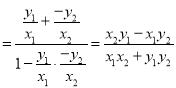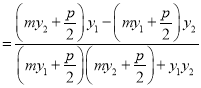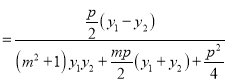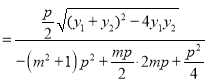故tan∠MON的取值范围是（﹣∞，]