题目内容
已知实数a>0,函数f(x)=
+a
.
(1)当a=1时,求f(x)的最小值;
(2)当a=1时,判断f(x)的单调性,并说明理由;
(3)求实数a的范围,使得对于区间[-
,
]上的任意三个实数r、s、t,都存在以f(r)、f(s)、f(t)为边长的三角形.
|
|
(1)当a=1时,求f(x)的最小值;
(2)当a=1时,判断f(x)的单调性,并说明理由;
(3)求实数a的范围,使得对于区间[-
2
| ||
| 5 |
2
| ||
| 5 |
由题意,f(x)的定义域为(-1,1),且f(x)为偶函数.
(1)a=1时,f(x)=
+
=
…(2分)
∴x=0时,f(x)=
+
最小值为2.…(4分)
(2)a=1时,f(x)=
+
=
∴x∈[0,1)时,f(x)递增;x∈(-1,0]时,f(x)递减;…(6分)
由于f(x)为偶函数,
∴只对x∈[0,1)时,说明f(x)递增.
设0≤x1<x2<1,
∴
>
>0,得
<
f(x1)-f(x2)=
-
<0
∴x∈[0,1)时,f(x)递增;…(10分)
(3)设t=
,则
∵x∈[-
,
],
∴t∈[
,1],∴y=t+
(
≤t≤1)
从而原问题等价于求实数a的范围,使得在区间[
,1]上,恒有2ymin>ymax.…(11分)
①当0<a≤
时,y=t+
在[
,1]上单调递增,∴ymin=3a+
,ymax=a+1,由2ymin>ymax得a>
,
从而
<a≤
;…(12分)
②当
<a≤
时,y=t+
在[
,
]上单调递减,在[
,1]上单调递增,∴ymin=2
,ymax=max{3a+
,a+1}=a+1,
由2ymin>ymax得7-4
<a<7+4
,从而
<a≤
;…(13分)
③当
<a<1时,y=t+
在[
,
]上单调递减,在[
,1]上单调递增,∴ymin=2
,ymax=max{3a+
,a+1}=3a+
,
由2ymin>ymax得
<a<
,从而
<a<1;…(14分)
④当a≥1时,y=t+
在[
,1]上单调递减,∴ymin=a+1,ymax=3a+
,
由2ymin>ymax得a<
,从而1≤a<
;…(15分)
综上,
<a<
.…(16分)
(1)a=1时,f(x)=
|
|
| 2 | ||
|
∴x=0时,f(x)=
|
|
(2)a=1时,f(x)=
|
|
| 2 | ||
|
∴x∈[0,1)时,f(x)递增;x∈(-1,0]时,f(x)递减;…(6分)
由于f(x)为偶函数,
∴只对x∈[0,1)时,说明f(x)递增.
设0≤x1<x2<1,
∴
1-
|
1-
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
∴x∈[0,1)时,f(x)递增;…(10分)
(3)设t=
|
∵x∈[-
2
| ||
| 5 |
2
| ||
| 5 |
∴t∈[
| 1 |
| 3 |
| a |
| t |
| 1 |
| 3 |
从而原问题等价于求实数a的范围,使得在区间[
| 1 |
| 3 |
①当0<a≤
| 1 |
| 9 |
| a |
| t |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 15 |
从而
| 1 |
| 15 |
| 1 |
| 9 |
②当
| 1 |
| 9 |
| 1 |
| 3 |
| a |
| t |
| 1 |
| 3 |
| a |
| a |
| a |
| 1 |
| 3 |
由2ymin>ymax得7-4
| 3 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
③当
| 1 |
| 3 |
| a |
| t |
| 1 |
| 3 |
| a |
| a |
| a |
| 1 |
| 3 |
| 1 |
| 3 |
由2ymin>ymax得
7-4
| ||
| 9 |
7+4
| ||
| 9 |
| 1 |
| 3 |
④当a≥1时,y=t+
| a |
| t |
| 1 |
| 3 |
| 1 |
| 3 |
由2ymin>ymax得a<
| 5 |
| 3 |
| 5 |
| 3 |
综上,
| 1 |
| 15 |
| 5 |
| 3 |

练习册系列答案
相关题目
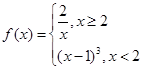 若关于
若关于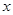 的方程
的方程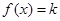 有两个不同的实根,则实数
有两个不同的实根,则实数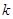 的取值范围是________.
的取值范围是________.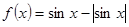 的性质,
的性质,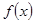 是以
是以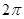 为周期的周期函数 ②
为周期的周期函数 ②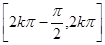 ,
,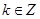
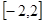 ④
④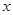 的取值集合为
的取值集合为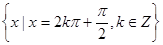
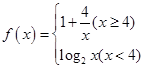 ,若关于
,若关于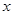 的方程
的方程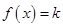 有两个不同的根,则实数
有两个不同的根,则实数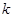 的取值范围是( )
的取值范围是( )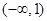
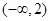
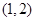
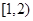
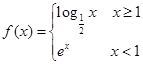 的值域为( )
的值域为( )