题目内容
已知函数f(x)=sin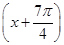 +cos
+cos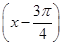 ,x∈R.
,x∈R.
(1)求f(x)的最小正周期和最小值;
(2)已知cos(β-α)=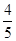 ,cos(β+α)=-
,cos(β+α)=-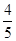 ,0<α<β≤
,0<α<β≤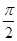 ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0.
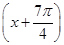 +cos
+cos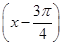 ,x∈R.
,x∈R.(1)求f(x)的最小正周期和最小值;
(2)已知cos(β-α)=
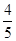 ,cos(β+α)=-
,cos(β+α)=-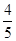 ,0<α<β≤
,0<α<β≤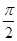 ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0.(1)-2(2)0
(1)解:f(x)=sinxcos +cosxsin
+cosxsin +cosxcos
+cosxcos +sinxsin
+sinxsin =
= sinx-
sinx- cosx=2sin
cosx=2sin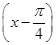 ,所以T=2π,f(x)min=-2.
,所以T=2π,f(x)min=-2.
(2)证明:cos(β-α)=cosαcosβ+sinαsinβ=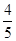 ,①
,①
cos(β+α)=cosαcosβ-sinαsinβ=-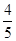 .②
.②
①+②,得cosαcosβ=0,
于是由0<α<β≤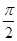 cosβ=0 β=
cosβ=0 β=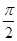 .
.
故f(β)= [f(β)]2-2=0
[f(β)]2-2=0
 +cosxsin
+cosxsin +cosxcos
+cosxcos +sinxsin
+sinxsin =
= sinx-
sinx- cosx=2sin
cosx=2sin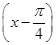 ,所以T=2π,f(x)min=-2.
,所以T=2π,f(x)min=-2.(2)证明:cos(β-α)=cosαcosβ+sinαsinβ=
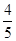 ,①
,①cos(β+α)=cosαcosβ-sinαsinβ=-
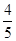 .②
.②①+②,得cosαcosβ=0,
于是由0<α<β≤
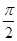 cosβ=0 β=
cosβ=0 β=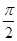 .
.故f(β)=
 [f(β)]2-2=0
[f(β)]2-2=0
练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
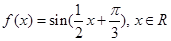 。
。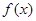 的单调递减区间;
的单调递减区间;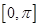 上的最大值及最小值;
上的最大值及最小值;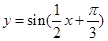 的图象作怎样的变换可得到
的图象作怎样的变换可得到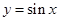 的图象?
的图象?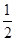 cos4x.
cos4x.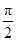 ,π),且f(α)=
,π),且f(α)=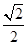 ,求α的值.
,求α的值.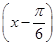 的图象,则φ=________.
的图象,则φ=________. sin
sin +
+ sinxcosx(x∈R).
sinxcosx(x∈R). 的值;
的值; =1,求sinB+sinC的最大值.
=1,求sinB+sinC的最大值. .
.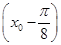 =-
=- ,求f(x0)的值.
,求f(x0)的值. 的最小正周期为π,且f
的最小正周期为π,且f =
= .
.
 ,求x的取值范围.
,求x的取值范围.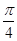 ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值; ,且a⊥c,求tan 2α的值.
,且a⊥c,求tan 2α的值. ,x∈R)的图象的一部分如图所示.
,x∈R)的图象的一部分如图所示.
 ]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.