题目内容
函数f(x)=sin sin
sin +
+ sinxcosx(x∈R).
sinxcosx(x∈R).
(1)求f 的值;
的值;
(2)在△ABC中,若f =1,求sinB+sinC的最大值.
=1,求sinB+sinC的最大值.
 sin
sin +
+ sinxcosx(x∈R).
sinxcosx(x∈R).(1)求f
 的值;
的值;(2)在△ABC中,若f
 =1,求sinB+sinC的最大值.
=1,求sinB+sinC的最大值.(1)1(2)

(1)f(x)=sin sin
sin +
+ sinxcosx=
sinxcosx=
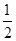 cos2x+
cos2x+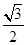 sin2x=sin
sin2x=sin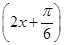 ,所以f
,所以f =1.
=1.
(2)因为f =1,所以sin
=1,所以sin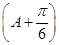 =1.
=1.
因为0<A<π,所以A+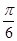 =
=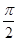 ,即A=
,即A=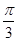 .
.
sinB+sinC=sinB+sin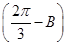 =
=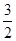 sinB+
sinB+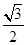 cosB=
cosB= sin
sin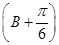 .
.
因为0<B<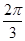 ,所以
,所以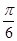 <B+
<B+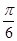 <
<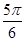 ,所以
,所以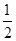 <sin
<sin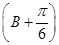 ≤1,
≤1,
所以sinB+sinC的最大值为 .
.
 sin
sin +
+ sinxcosx=
sinxcosx=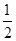 cos2x+
cos2x+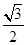 sin2x=sin
sin2x=sin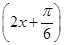 ,所以f
,所以f =1.
=1.(2)因为f
 =1,所以sin
=1,所以sin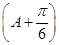 =1.
=1.因为0<A<π,所以A+
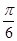 =
=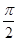 ,即A=
,即A=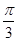 .
.sinB+sinC=sinB+sin
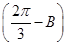 =
=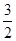 sinB+
sinB+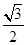 cosB=
cosB= sin
sin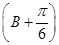 .
.因为0<B<
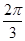 ,所以
,所以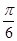 <B+
<B+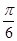 <
<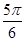 ,所以
,所以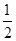 <sin
<sin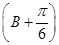 ≤1,
≤1,所以sinB+sinC的最大值为
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的部分图象如图示,则将
的部分图象如图示,则将 的图象向右平移
的图象向右平移 个单位后,得到的图象解析式为( )
个单位后,得到的图象解析式为( )




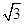 cos2x-
cos2x-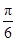 )-2m+3(m>0),若存在x1,x2∈[0,
)-2m+3(m>0),若存在x1,x2∈[0,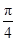 ],使得f(x1)=g(x2)成立,则实数m的取值范围是 .
],使得f(x1)=g(x2)成立,则实数m的取值范围是 .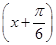 ,其中x∈
,其中x∈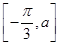 ,若f(x)的值域是
,若f(x)的值域是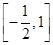 ,则a的取值范围是________.
,则a的取值范围是________.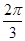 .
.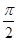 个单位长度得到,求y=g(x)的单调增区间.
个单位长度得到,求y=g(x)的单调增区间.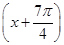 +cos
+cos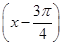 ,x∈R.
,x∈R.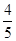 ,cos(β+α)=-
,cos(β+α)=-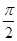 ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0.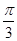 ,则f
,则f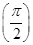 =________.
=________. 在
在 上单调递减,则
上单调递减,则 可以是( )
可以是( )


 ]上有零点,则实数m的取值范围为( )
]上有零点,则实数m的取值范围为( )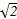 ]
]