题目内容
已知函数f(x)=(2cos2x-1)sin2x+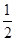 cos4x.
cos4x.
(1)求f(x)的最小正周期及最大值;
(2)若α∈(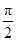 ,π),且f(α)=
,π),且f(α)=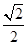 ,求α的值.
,求α的值.
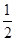 cos4x.
cos4x.(1)求f(x)的最小正周期及最大值;
(2)若α∈(
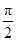 ,π),且f(α)=
,π),且f(α)=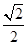 ,求α的值.
,求α的值.(1) f(x)的最小正周期为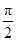 ,最大值为
,最大值为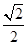 (2)
(2) 
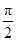 ,最大值为
,最大值为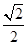 (2)
(2) 
解:(1)因为f(x)=(2cos2x-1)sin2x+
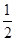 cos4x
cos4x=cos2xsin2x+
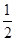 cos4x
cos4x=
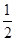 (sin4x+cos4x)
(sin4x+cos4x)=
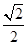 sin(4x+
sin(4x+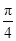 ),
),所以f(x)的最小正周期为
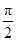 ,最大值为
,最大值为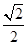 .
.(2)因为f(α)=
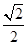 ,所以sin(4α+
,所以sin(4α+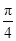 )=1.
)=1.因为α∈(
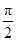 ,π),
,π),所以4α+
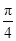 ∈(
∈( ,
,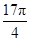 ).
).所以4α+
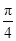 =
= .故α=
.故α= .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
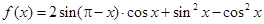 ,
,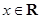 .
.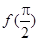 的值及函数
的值及函数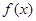 的最小正周期;
的最小正周期;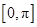 上的单调减区间.
上的单调减区间.
 取得最小值时θ的值.
取得最小值时θ的值.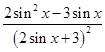 的值域为 .
的值域为 .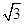 cos2x-
cos2x-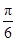 )-2m+3(m>0),若存在x1,x2∈[0,
)-2m+3(m>0),若存在x1,x2∈[0,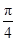 ],使得f(x1)=g(x2)成立,则实数m的取值范围是 .
],使得f(x1)=g(x2)成立,则实数m的取值范围是 .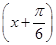 ,其中x∈
,其中x∈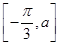 ,若f(x)的值域是
,若f(x)的值域是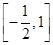 ,则a的取值范围是________.
,则a的取值范围是________.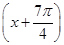 +cos
+cos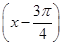 ,x∈R.
,x∈R.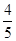 ,cos(β+α)=-
,cos(β+α)=-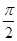 ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0. ,直线x=
,直线x= 是其图象的一条对称轴,则符合条件的解析式为( )
是其图象的一条对称轴,则符合条件的解析式为( )

 +2
+2